Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Методом последовательных приближений .

При траектории необходимо знать следующие параметры траектории движения ракеты в зависимости от времени:

§ Скорость V=V(t);

§ Дальность X=X(t);

§ Высота Y=Y(t);

§ Угол траектории Θ =Θ (t).

Допущения для данной задачи:

1. Траектория полета ракеты плоская кривая.

2. Пренебрегаем кривизной Земли в пределах дальности АУТ.

3. Силу тяжести считаем постоянной, т.е. g = const.

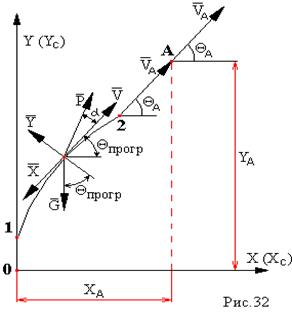
Таким образом траекторию активного участка можно показать так (рис.32):

01 – вертикальный участок траектории;

12 – программный участок траектории;

2А – наклонный (или прямой) участок траектории.

В качестве критерия точки 1 служит скорость, которая должна быть достигнута ракетой в этой точке (≈ 55 м/с). На программном участке траектории угол Θ =Θ _прогр.

Θ _прогр=At²+Bt+C - задается в общем виде.

Коэффициенты А, В, С определяются из трех граничных условий в точках 1 и 2.

точка 1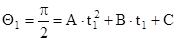

точка 2 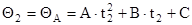находим А, В, С имея ввиду,

точка 2 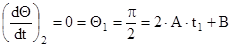что Θ _А дано.

Таким образом необходимо определить параметры движения ракеты на активном участке. Для этого составим систему уравнений:

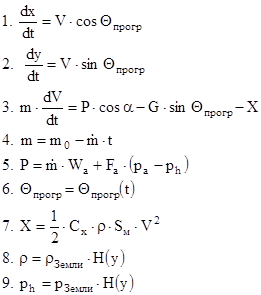
где Н(у) – функция, зависящая от высоты полета;

р_Земли =101340 .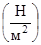

Т.к. α для БР при их движении на АУТ небольшой (α ≤ 10^о), то можно принять, что

cosα ≈ 1; sin α ≈ α. Приведенная выше система является нелинейной, замкнутой и ее можно решить любым численным методом.