💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Регистр флагов

Лекция № 7 (90-минут)

Тема: КОДИРОВАНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ

В связи с тем, что алгоритмы выполнения операций в компьютерных системах имеют свою специфику, возникает проблема представления отрицательных чисел.

Ее решают за счет использования особых способов кодирования числовых данных.

Рассмотрим три наиболее распространенных кода, которые применяются на практике: - прямой код; - обратный код; - дополнительный код.

Прямой код используется для представления отрицательных чисел в запоминающем устройстве компьютерной системы, а также при умножении и делении.

Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока компьютерной системы.

К кодам выдвигаются следующие требования:

- разряды числа в коде жестко связаны с определенной разрядной сеткой;

- для записи кода знака в разрядной сетке отводится фиксированный, строго определенный разряд.

1. Прямой код. Наиболее естественный код. Формируется следующим образом: в знаковый бит (S_X) числа помещают знак числа (0 - если число положительное и 1 - если число отрицательное), а остальные биты используют для абсолютного значения (модуля) числа. Правило преобразования чисел в прямом коде можно записать так:

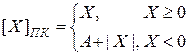. (3.8)

где A - вес старшего разряда в n-разрядной сетке, A=2^s-1.

Отображение (s-битных) наборов (прямой код, верхняя числовая прямая) на числовую ось (числа, нижняя числовая прямая) для компьютерной системы показано на рис. 3.3

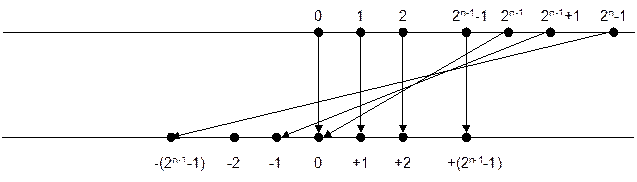
Рисунок 3.3- Отображение s-битных наборов (прямой код) на числовую ось

Например:

Диапазон представимых чисел: -(2^s-1-1)…(2^s-1).

Положительный момент заключается в удобстве операции ввода-вывода данных. Отрицательный момент в том, что существует два представления (0) и операция алгебраического сложения требует анализа знаков и модулей операндов, и выбора фактической операции сложения или вычитания.

2. Обратный код. Обратный (n - разрядный) двоичный код положительного целого числа состоит из одноразрядного кода знака (0), за которым следует (n - 1) разрядное двоичное представление модуля числа, то есть обратный код для положительного числа совпадает с прямым кодом.

Обратный (n - разрядный) двоичный код отрицательного целого числа состоит из одноразрядного кода знака (1), за которым следует (n - 1) разрядное двоичное число, представляющее собой инвертированное (n - 1) разрядное представление модуля числа, то есть для отрицательного числа все цифры числа заменяются на противоположные, а именно (1 на 0, а 0 на 1) и в знаковый разряд заносится единица.

Обратный код числа определяется соотношением:

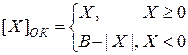. (3.9)

где B=2^s-1=X_max - максимальное число в n-разрядной сетке.

Отображение (s-битных) наборов (обратный код, верхняя числовая прямая) на числовую ось (числа, нижняя числовая прямая) для компьютерной системы показано на рис. 3.4.

Рисунок 3.4 - Отображение s-битных наборов (обратный код) на числовую ось

Например:

Диапазон представимых чисел: -(2^s-1-1)…(2^s-1).

Положительный момент заключается в том, что при сложении обратных кодов чисел как беззнаковых чисел получаем обратный код суммы.

Отрицательный момент заключается в том, что существует два представления (0) и при выполнении операций сложения в обратном коде требуется коррекция суммы с помощью циклического переноса единицы переполнения из знаковых разрядов суммы.

3. Дополнительный код. Наиболее распространенный способ представления отрицательных целых чисел в компьютерных системах.

Он позволяет заменить операцию вычитания на операцию сложения, чем упрощает архитектуру компьютерной системы.

Дополнительный код является дополнением числа до некоторого граничного числа (|X_max+1|=2^s).

Дополнительный код положительного числа совпадает с прямым кодом.

Для получения дополнительного кода отрицательного числа существует три способа:

- все цифры модуля исходного числа заменяются на взаимно обратные, то есть производится инверсия всех цифр числа, затем к полученному значению добавляется единица в младшем разряде;

- из модуля числа вычитается (1) младший бит, а затем инвертируются все разряды;

- необходимо записать n-битный модуль числа. Затем просматривать число справа налево, сохранить все младшие нули и первую встретившуюся (1), а остальные биты инвертировать.

Дополнительный код числа определяется соотношением:

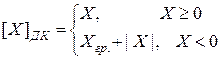. (3.10)

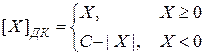. (3.11)

где - 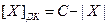, C = X_гр. равняется весу не существующего в данном числе разряда, расположенного слева от знаковой цифры.

Отображение s-битных наборов (дополнительный код верхняя числовая прямая) на числовую ось (числа нижняя числовая прямая) для компьютерной системы показано на рис. 3.5.

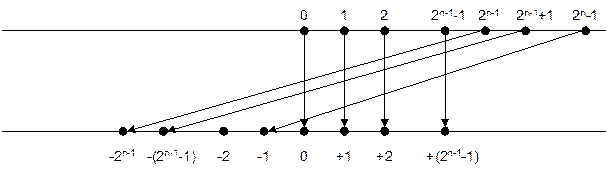
Рисунок 3.5 - Отображение s-битных наборов (дополнительный код) на числовую ось

Например:

Диапазон представимых чисел: -(2^s-1)…(2^s-1).

Свойства дополнительного кода:

- при сложении чисел в дополнительном коде как беззнаковых чисел получаем дополнительный код суммы. Знаковые биты суммируются обычным образом, а возникающий при их сложении перенос игнорируется.

- любое число в дополнительном коде можно считать младшими битами («хвостом») числа любой длины, если содержимое знакового бита копировать влево. Эта операция называется расширением знака. Используется, когда исходные операнды в операциях сложения и вычитания имеют разную длину.

Свойства кодов:

1. Операции должны выполняться над данными, представленными в одном и том же коде: ПК-ПК, ОК-ОК, ДК-ДК;

2. Положительные числа в ПК, ОК, ДК не меняют своего представления;

3. Результат выполнения операций сложения и вычитания над числами, представленными в ПК, ОК или ДК, являются ПК, ОК или ДК соответственно;

4. Двоичный набор, представляющий (-0) в ПК и ДК, является запрещенной комбинацией;

5. В отличие от ПК, в ОК и ДК нельзя отбрасывать нули после знакового разряда в целой части и нули в конце дробной части отрицательного числа (разрешается отбрасывать 1).

Лекция № 8 (90-минут)