Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Тема: системы счисления

Система счисления - совокупность приемов и правил для установления однозначного соответствия между любым числом и его представлением в виде некоторой совокупности знаков (символов). Запись числа в некоторой системе счисления называют кодом числа. Кратко число записывается следующим образом:

.

где: А_КЭЧ - количественный эквивалент числа (А);

(a_na_n-1….a₂a₁a₀) - цифры из множества, с помощью которых можно представить число (А);

n - количество разрядов в числе.

Например:

Отдельную позицию в изображении числа принято называть разрядом, а номер позиции - номером разряда. Число разрядов в записи числа называется разрядностью и совпадает с его длиной.

Тогда количественный эквивалент числа - (КЭЧ) - (А), заданного в определенной системе счисления, является некоторой функцией числовых эквивалентов всех его цифр, т.е.:

.

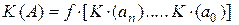где: К(А) - количественный эквивалент числа (А);

К (а_n) - максимальный количественный (числовой) эквивалент цифры числа (А), находящийся в крайнем левом разряде;

К (а₀) - минимальный количественный (числовой) эквивалент цифры числа (А), находящийся в крайнем правом разряде;

Следовательно при любой конечной разрядной сетке КЭЧ (А) будет принимать в зависимости от количественных эквивалентов отдельных разрядов значения от К(А)_min до К(А)_max.

.

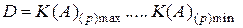где: D - диапазон представимых чисел в определенной системе счисления;

К(А)_(р)max - максимальный количественный эквивалент числа (А) по основанию (р);

К(А)_(р)mіn - минимальный количественный эквивалент числа (А) по основанию (р).

Любая система счисления, предназначенная для практического использования, должна обеспечивать:

- возможность представления любого числа в заданном диапазоне чисел;

- однозначность представления;

- краткость и простоту записи чисел;

- легкость овладения системой, а также простоту и удобство оперирования ею.

2.1 Классификация систем счисления

В настоящее время различают позиционные и непозиционные системы счисления. Классификация систем счисления приведена на рис. 2.1.

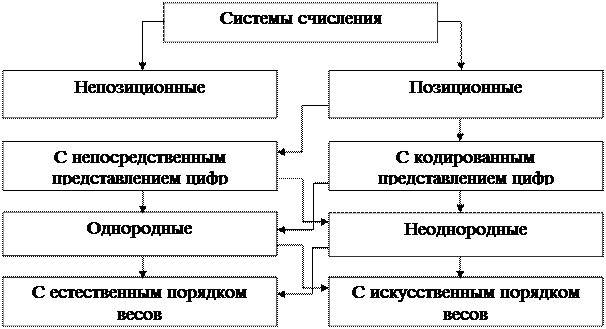Непозиционная система счисления: это такая система счисления, в которой каждой цифре на любом ее месте в записи числа однозначно соответствует один и тот же количественный эквивалент.

Наиболее известным примером такой системы является римская система счисления:

В римской системе счисления несколько стоящих рядом одинаковых цифр суммируются:

XXX = X+X+X= 30₍₁₀₎.

Если рядом стоят разные цифры, причем младшая – справа от старшей, то они также суммируются:

XVI = X+V+I = 16₍₁₀₎.

Если же младшая цифра находится слева от старшей, то она вычитается из этой старшей цифры:

IX = X – I = 9₍₁₀₎.

Недостатки римской системы счисления заключаются в следующем:

- в пределе, теоретически, она имеет бесконечное количество цифр;

- арифметические действия над числами очень сложны;

- отсутствует цифра {0}.

Позиционная система счисления: это такая система счисления, в которой одной и той же цифре в зависимости от ее местоположения в записи числа соответствуют различные количественные эквиваленты. Наиболее известным примером такой системы является десятичная система счисления, например: цифры 1 и 2 в зависимости от местоположения этих цифр в числе изменяется значение самого числа:

При таком положении цифр получается число двенадцать (12₍₁₀₎).

Если поменять местами цифры 1 и 2:

получается число двадцать один (21₍₁₀₎).

Любое число в позиционной системе счисления может быть записано в виде:

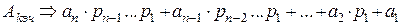. (2.4)

где - количественный эквивалент числа (А), состоящего из (n) цифр;

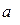- цифра, ;

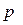- основание системы счисления.

Правило: Количественный эквивалент числа в позиционной системе счисления равен сумме произведений количественных значений цифр и степеней основания, показатели которых равны номерам разрядов, причем нумерация разрядов начинается с (0).

Например: 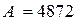, n=4, p=10, тогда можно записать:

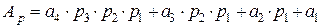. (2.5)

тогда:

.

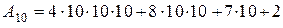Однородность системы счисления означает, что во всех разрядах числа, записанного в такой системе, используют цифры из одного и того же множества.

Например, в обычной десятичной системе счисления во всех разрядах числа используются цифры из множества:

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9},

в двоичной системе счисления используются цифры из множества:

{0, 1},

в троичной системе счисления используются цифры из множества:

{0, 1, 2},

в пятеричной системе счисления используются цифры из множества:

{0, 1, 2, 3, 4},

в восьмеричной системе счисления используются цифры из множества:

{0, 1, 2, 3, 4, 5, 6, 7},

в шестнадцатеричной системе счисления при записи числа используются цифры и буквы:

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}.

Если позиционная система счисления однородная с непосредственным представлением цифр и с естественным порядком весов, то любое число может быть представлено в виде суммы попарных произведений:

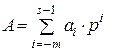. (2.6)

где - количественный эквивалент числа (А);

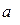- цифра,

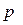- основание системы счисления.

s - количество разрядов в целой части числа слева от запятой;

m - количество разрядов в дробной части числа справа от запятой.

Исходя из выше сказанного можно записать:

.

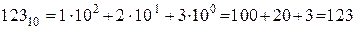или: .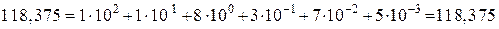

Соответствие чисел в (10 - ой), (16 – ой), (8 – ой) и (2 – ой) системах счисления приведены в таблице:

Таблица - Соответствие чисел в (10 - ой), (16 - ой), (8 - ой) и (2 - ой) системах счисления

Помимо позиционных однородных систем известны также позиционные неоднородные (смешанные) системы счисления.

В таких системах цифры в разных разрядах могут принимать значения из различных множеств.

Задают неоднородные системы с помощью двухстрочных матриц вида:

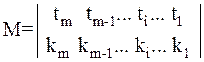. (2.7)

Здесь в первой строке матрицы указано число разрядов (t_i), отводимых в (i-й) группе разрядов (i= 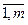) представления числа для записи цифр по основанию (k_i), которое указано во второй строке того же столбца.

Лекция №3 (90-минут)