Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: продолжение Лекции №2
|
|
Неоднородные системы счисления, так же как и однородные, могут быть с непосредственным и с кодированным представлением цифр.
Примером смешанной системы с кодированным представлением цифр является система измерения времени (в годах, месяцах, неделях, сутках, часах, минутах и секундах).
Например: надо выразить время в 2- года, 25 - суток, 14 - часов, 35- минут и 48 секунд, в секундах. Тогда можно записать, что основание в каждом разряде равно:
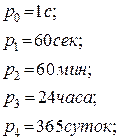
цифры имеют следующие значения:
По формуле можно записать:
.
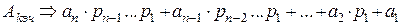
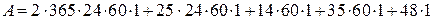Существует так же неоднородная двоично-пятиричная система счисления, в которой в нечетных разрядах основание р1=5, (аі= 0 - 4), а в четных разрядах основание р2=2, (аі= 0, 1).
Так как произведение весов двух соседних (четного и нечетного) разрядов равно десяти, то двумя двоично-пятиричными разрядами можно кодировать одну десятичную цифру.
Таблица 2.2 - Пример записи десятичных цифр в двоично-пятиричной системе
| а(10) | а(2-5) | а(10) | а(2-5) |
Например: записать число 853(10) в двоично-пятиричной системе счисления.
Решение: исходя из значений, представленных в табл. 2.2 имеем:
| 8(10)=13(2-5) |
| 5(10)=10(2-5) |
| 3(10)=03(2-5) |
тогда: 853(10) = 13 10 03(2-5).
Существует так же кодированные системы счисления - это позиционные системы счисления, в которых цифры одной системы счисления кодируются при помощи цифр другой системы, а число в общем виде записывается следующим образом:
.
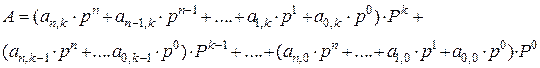где: А - число;
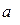- цифры из множества, с помощью которых можно записать число (А);
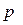- основание системы счисления, символами которой кодируются цифры;
Р - основание исходной системы счисления.
Классическим примером кодированной системы счисления есть – двоично-десятичная система.
При двоично-десятичном кодировании каждая десятичная цифра заменяется тетрадой (четверкой) двоичных цифр, а сами тетрады записываются последовательно в соответствии с порядком следования десятичных цифр.
При обратном преобразовании двоично-десятичного кода в десятичный исходный код разбивается на тетрады вправо и влево от запятой, которые затем заменяются десятичными цифрами.
Например: десятичное число 12(10) записать в двоично-десятичной системе счисления = 0001 0010(2-10).
При построении кодированных позиционных систем счисления в качестве весов разрядов могут быть выбраны как члены геометрической прогрессии, так и произвольные числа.
В зависимости от этого кодированные системы счисления делятся на кодированные системы счисления с естественными разрядами весов и на кодированные системы счисления с искусственными разрядами весов.
Кодированные системы счисления с естественными разрядами весов – это позиционная система счисления, в которой в качестве весов разрядов используются члены геометрической прогрессии.
Примером системы счисления с естественными разрядами весов может служить двоично-десятичная система с весами (8-4-2-1).
Кодированные системы счисления с искусственными разрядами весов – это позиционная система счисления, в которой в качестве весов разрядов используются произвольные числа.
Примером системы счисления с искусственными разрядами весов может служить двоично-десятичная система с весами (2-4-2-1, 5-2-1-3).
Искусственный порядок весов широко применяется в аналогово-цифровых и цифро-аналоговых преобразователях.
В табл. 2.3 представлены числа, записанные в десятичной системе счисления и в кодированной системе счисления с естественным и искусственным порядком весов.
Таблица 2.3 - Числа десятичной системы счисления и кодированной системе счисления с естественным и искусственным порядком весов.
| Десятичная СС | Кодированная СС 8-4-2-1 | Кодированная СС 4-2-2-1 | Кодированная СС 2-4-2-1 |
Например: десятичное число 1593(10) в двоично-десятичной системе счисления с естественными разрядами весов 8-4-2-1 имеет вид: 0001 0101 1001 0011, а в двоично-десятичной системе счисления с искусственными разрядами весов 2-4-2-1 имеет вид: 0001 0101 1111 0011.
В современных компьютерных системах помимо рассмотренных систем счисления встречаются и системы счисления с непостоянными разрядами весов. Наиболее известным примером таких систем является код Грея.
Кодом Грея порядка (n) называется любая циклическая последовательность всех наборов из (0) и (1) длины (n), в которой два соседних набора отличаются ровно в одной компоненте.
Код Грея является одношаговым кодом, т.е. при переходе от одного числа к другому всегда меняется лишь какой то один из всех битов. Соответствие десятичных чисел в диапазоне от 0 до 15 двоичным числам и коду Грея приведено в табл. 2.4.
В двоичном коде при переходе от изображения одного числа к изображению соседнего числа может происходить одновременное изменение цифр в нескольких разрядах, что может явиться источником ошибок, в работе аппаратуры в некоторых случаях например при переходе от 7 к 8.
В коде Грея два соседних значения отличаются только в одном разряде.
Двоичные разряды в коде Грея не имеют постоянного веса. Код Грея изначально предназначался для защиты от ложного срабатывания электрических переключателей и широко используется для упрощения выявлений и исправления ошибок в системах связи.
Таблица - Соответствие десятичных чисел в диапазоне от 0 до 15 двоичным числам и коду Грея
| Десятичные числа | Двоичные числа | Код Грея |
Лекция №4 (45-минут)
|
|