
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: выбор системы счисления для использования в компьютерной системе
|
|
Непозиционные системы счисления непригодны в силу своей громоздкости и трудности выполнения арифметических операций.
Из позиционных систем счисления наиболее удобны однородные системы счисления, так как одинаковое основание, т.е. одинаковое количество символов во всех разрядах приводит к наиболее рациональному использованию оборудования и наиболее простым алгоритмам выполнения арифметических операций. Поэтому проанализируем однородные позиционные системы счисления на предмет их применения в компьютерных системах. При этом будем учитывать следующие факторы:
- простота технической реализации. Очевидно, что (р - позиционный) запоминающий элемент будет тем проще, чем меньше состояний (позиций) ему требуется иметь, т.е. чем меньше основание системы счисления.
- наибольшая помехоустойчивость кодирования цифр. Исходя из условия равных технических возможностей при реализации любой системы счисления, будем считать, что диапазон изменения носителя информации для всех систем остается одинаковым. Если увеличить диапазон некоторого носителя информации при реализации одной системы счисления, то его можно увеличить и при реализации другой системы. Но тогда очевидно преимущество систем с малыми основаниями, так, как представления цифр в этих системах отличаются друг от друга в более значительной степени, чем в системах с большими основаниями. Это значит, что при наложении на основной сигнал, изображающий цифру, некоторой помехи произвольной формы, наибольшая ошибка возможна в устройстве, использующем систему счисления с самым большим основанием.
- минимум оборудования. Чтобы решить, какой системе отдать предпочтение с точки зрения получения минимума расхода оборудования при прочих равных условиях, сделаем предположение, что все машины оперируют с одним и тем же количеством чисел. Если (bi) – количество цифр, с которыми оперирует (i-я) машина; (ni) - количество разрядов, в каждом числе (i-ой) машины, то произведение:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
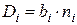 . (2.9)
. (2.9)
где Di - количество цифроразрядов, приходящихся на 1 число;
bi - количество цифр;
ni - количество разрядов.
Таким образом, задача в данном случае сводится к нахождению такой системы счисления, которая имеет самое малое количество цифроразрядов при заданном количестве чисел – операндов (N):
 . (2.10)
. (2.10)
формулу (2.10) можно переписать в другом виде:
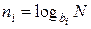 . (2.11)
. (2.11)
подставив это значение (ni) в соотношение (2.9), получим:
 . (2.12)
. (2.12)
будим считать, что основание системы счисления может принимать любые значения, не только целочисленные, изменяясь непрерывно а не дискретно.
Тогда количество цифроразрядов также будет величиной непрерывной, связанной с основанием системы счисления логарифмической функциональной зависимостью:
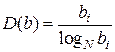 . (2.13)
. (2.13)
теперь задача нахождения D(b)min.сводится к обыкновенному исследованию функции (2.13) на экстремум:
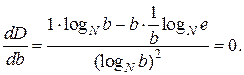 (2.14)
(2.14)
откуда 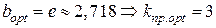 . Выясним теперь, насколько каждое из целочисленных оснований (bi) уступает (bopt) Для этого оценим каждое основание (bi) не абсолютной величиной (Di), а его относительным значением:
. Выясним теперь, насколько каждое из целочисленных оснований (bi) уступает (bopt) Для этого оценим каждое основание (bi) не абсолютной величиной (Di), а его относительным значением:
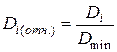 . (2.15)
. (2.15)
где:
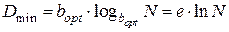 (2.16)
(2.16)
Подставив выражение (2.16) в формулу (2.15), получим выражение, не зависящее от величины (N):
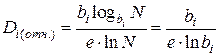 . (2.17)
. (2.17)
Произведя расчеты по формуле (2.17) для некоторых оснований системы счисления, сведем полученные результаты в табл. 2.5:
Таблица 2.5 - Соотношение оснований систем счисления и эффективности
| bi | |||||||||
| Di(отн.) | 1, 062 | 1, 004 | 1, 062 | 1, 143 | 1, 232 | 1, 3 | 1, 416 | 1, 507 | 1, 597 |
- простота арифметических действий. Чем меньше цифр в системе счисления, тем проще арифметические действия. Таблицы сложения, вычитания, умножения и деления будут усложняться с увеличением основания системы счисления.
- наибольшее быстродействие. Более сложные операции такие как умножение и деление, расчленяются на более простые операции такие как операции сложения и сдвига. С увеличением основания системы счисления быстродействие будет падать.
- простота формального аппарата для синтеза цифровых устройств.
Математическим аппаратом, позволяющим относительно просто и экономично строить цифровые схемы, узлы, блоки, является алгебра логики.
Наибольшее развитие и законченность вследствие своей простоты и широкого практического распространения двухпозиционных элементов в настоящее время получила двузначная логика.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
- удобство работы. Безусловно наилучшейсистемой счисления с точки зрения удобства работы человека является десятичная, так как в любом другом случае потребуется переводить исходные числа из десятичной системы в принятую, а затем обратно в десятичную. Поэтому можно утверждать, что все системы счисления с основаниями превышающими десятичную систему счисления, являются менее удобными, чем системы с малыми основаниями.
В соответствии с рассмотренными критериями формируется комплексный показатель. При этом максимальную оценку получает система счисления с основанием два. Это позиционная система счисления, в которой для изображения чисел используются два символа, а веса разрядов меняются по закону (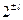 ).
).
Большой практический интерес представляют двоично-кодированные системы счисления: двоично - десятичная Binary Code Decimal (BCD), восьмеричная (octal), шестнадцатеричная (hexadecimal). В них каждый разряд записывается с помощью нескольких двоичных разрядов, имеющих определенные веса. Цифры восьмеричной системы представляются тремя двоичными разрядами (триадами), десятичной и шестнадцатеричной - четырьмя (тетрадами). Также следует отметить, что восьме- и шестнадцатеричные системы относятся к особому классу систем с основанием кратным (2). Эта особенность обуславливает их широкое применение в процессе взаимодействия с пользователем компьютерной системы. С одной стороны, они облегчают восприятие двоичной информации, т.к. любое двоичное представление числа может быть разбито на триады или тетрады, которые проще для визуального восприятия человеком. С другой стороны, они часто используются в качестве промежуточных систем счисления при переводе из десятичной системы счисления в двоичную систему счисления и наоборот.
Двоичная система счисления вводит понятие основной структурной единицы информации, которой является бит (bit - bi nary digi t). Бит соответствует одному двоичному разряду числа, представленного в двоичной системе счисления.
Однако бит является слишком мелкой единицей и не всегда удобен для практических приложений. Поэтому наряду с битом в компьютерной системе получила распространение производная структурная единица информации - машинное слово, под которым понимают упорядоченную совокупность битов, имеющую некоторый смысл, т.е. воспринимаемую основными устройствами компьютера как единое целое. Длина машинного слова является одной из определяющих характеристик компьютерной системы и выбирается исходя, прежде всего, из соображений точности. Таким образом, длина машинного слова является различной для компьютерных систем разных классов. Для унифицированного представления информации используют машинно-независимую структурную единицу - байт - byte - (кусок, часть) - совокупность из восьми смежных двоичных разрядов. Длину машинного слова обычно выбирают равной целому числу байт. Восьмиразрядный байт удобен тем, что полностью покрывает всю символьную информацию и удобен для записи десятичных и 16-ричных тетрад.
Лекция №5 (90-минут)
|
|
