Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Схема 4

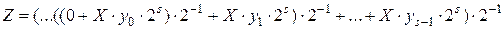. (4.16)

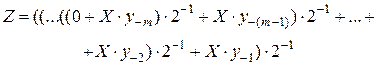. (4.17)

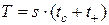. (4.18)

Рассмотрим на примере два базовых алгоритма умножения в компьютерных системах двоичных беззнаковых чисел:

Алгоритм №1. Алгоритм умножения младшими разрядами вперед, со сдвигом суммы ЧП вправо.

1. Исходное значение суммы (ЧП) принимается равным (0), счетчику тактов - (Сч.Т) присваивается значение, равное числу разрядов множителя.

2. Анализируется младшая разрядная цифра множителя. Если она равна (1), то к сумме (ЧП) прибавляется множимое, совмещенное по старшим разрядам; если (0) - прибавление не производится.

3. Производится сдвиг множителя и суммы ЧП вправо на (1) разряд. Содержимое (Сч.Т) уменьшается на (1).

4. Анализируется содержимое (Сч.Т). Если оно не равно (0), то переход к (п.2), иначе - (п.5).

5. Умножение закончено, младшая часть произведения находится на месте множителя, а старшая - на месте суммы (ЧП). Например: необходимо перемножить два беззнаковых числа (7∙ 3=21). Для удобства возьмем длину разрядной сетки равную четырем битам, а именно: Х = 7 - множимое, Y = 3 - множитель, Z = 21 - произведение. Если (X) и (Y) равняется четырем битам, то как было отмечено выше (Z) должно быть восьмиразрядным значением, т.е длина разрядной сетки произведения в два раза больше множимого и множителя. Алгоритм умножения приведен в табл. 4.1.

Таблица 4.1 - Алгоритм умножения со сдвигом вправо двоичных беззнаковых чисел

Алгоритм №2. Алгоритм умножения старшими разрядами вперед, со сдвигом суммы ЧП влево.

1. Исходное значение суммы (ЧП) принимается равным (0), (Сч.Т) присваивается значение, равное числу разрядов множителя.

2. Производится сдвиг суммы (ЧП) влево на (1) разряд.

3.Анализируется старшая разрядная цифра множителя. Если она равна (1), то к сумме (ЧП) прибавляется множимое, совмещенное по младшим разрядам; если (0) - прибавление не производится.

4.Производится сдвиг множителя влево на (1) разряд. Содержимое (Сч.Т) уменьшается на (1).

5.Анализируется содержимое (Сч.Т). Если оно не равно (0), то переход к (п.2), иначе - (п.6).

6.Умножение закончено, произведения находится на месте суммы (ЧП), которая имеет удвоенную разрядность. Например: необходимо перемножить два беззнаковых числа (7∙ 3=21). Для удобства возьмем длину разрядной сетки равную четырем битам, а именно: Х = 7 - множимое, Y = 3 - множитель, Z = 21 - произведение. Если (X) и (Y) равняется четырем битам, то как было отмечено выше (Z) должно быть восьмиразрядным значением, т.е длина разрядной сетки произведения в два раза больше множимого и множителя. Алгоритм умножения приведен в табл. 4.1.

Таблица 4.2 - Алгоритм умножения со сдвигом влево двоичных беззнаковых чисел

Лекция № 10 (90-минут)