
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Одночастотные вынужденные колебания. Частотные характеристики
|
|
f(t)=Bsinω t (6.1)
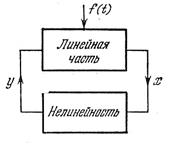
Рис.6.1
Уравнение динамики системы имеет вид
Q(p)x + R(p)F(x) = S(p)f(t) (6.2)
Решение для вынужденных колебаний будем искать приближенно в форме
x = α sin(ω t + φ) (6.3)
где ω задано, а неизвестными являются амплитуда α и фаза φ.
Произведем гармоническую линеаризацию нелинейности:
 (6.4)
(6.4)
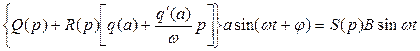 (6.5)
(6.5)
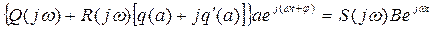
или
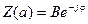 (6.6)
(6.6)
где
 (6.7)
(6.7)
Уравнение (6.6) с двумя неизвестными α и φ можно решить графически
 Рис.6.2
Рис.6.2
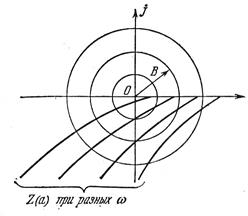
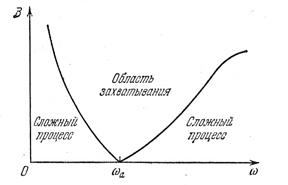
Рис. 6.3. Рис. 6.4.
На основании рис. 6.3 можно построить зависимости α (ω) и φ (ω), т. е. частотные характеристики замкнутой нелинейной системы по первой гармонике (6.3).

Рис.6.5
Пример. Пусть уравнение системы имеет вид

при гистерезисной нелинейности (рис. 6.6) и f(t)= Bsinω t. Тогда в уравнении (6.6), согласно (6.7), будем иметь
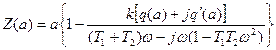
Для заданной частоты 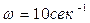 и заданных параметров системы k = 10, с = 10, b = 4, T1= 0, 01, Т2 = 0, 02, кривая Z(α) изображена на рис. 6.6, где отмечены значения α.
и заданных параметров системы k = 10, с = 10, b = 4, T1= 0, 01, Т2 = 0, 02, кривая Z(α) изображена на рис. 6.6, где отмечены значения α.

Рис. 6.6. Рис. 6.7.
Проведя окружности разных радиусов В, по точкам пересечения определим зависимости α (В) и φ (B) (рис. 6.7) для вынужденных колебаний при данной частоте.
|
|
