Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Определение периодического решения (автоколеба­ний).

Глава 3. Методы припасовывания и точечного преобразования

Метод припасовывания

Дана система, схема которой изображе­на на рис. 3.1, а, нелинейная характеристика F(x) регу­лятора представлена на рис. 3.1, б. Уравнение объекта:

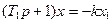
уравнение регулятора:

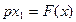
Общее уравнение замкнутой системы имеет вид

(3.1)

Определение переходного процесса. Представим себе примерно возможный качественный вид процесса (рис. 3.2). Он разбивается на участки АВ, BD и т. д.,

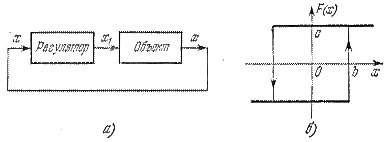
Рис.3.1

внутри которых в соответствии с нелинейной характеристикой функция F(x) принимает постоянные значения +с или —с. Изобразим отдельно

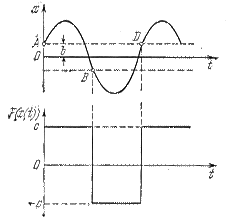
Рис.3.2

участки АВ и BD (рис. 3.3), отсчитывая время t на каждом из них от нуля.

На участке АВ, согласно (3.1), уравнение системы

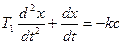
имеет первый интеграл в виде

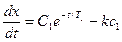(3.2)

а второй —

(3.3)

Рис.3.3

Определение периодического решения (автоколеба­ний).

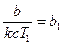
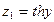
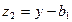
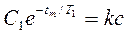
Рис.3.4

Далее по формуле (3.3) определим амплитуду автоко­лебаний:

где С₁ известно из (3.9). В результате формула

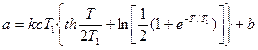
позволяет вычислить и амплитуду автоколебаний.