Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
-
Как продвинуть сайт на первые места?Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.Ускорение продвиженияЕсли вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги. Начать продвижение сайта
-
Сервис онлайн-записи на собственном Telegram-ботеТот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом -
Примеры точечного преобразования
|
|
Уравнения объекта и регулятора имеют вид
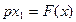
где F(x) — гистерезисная релейная характеристика (рис. 3.10). Эту систему уравнений перепишем в виде
(3.17)
Рис.3.10
На фазовой плоскости (х, у) нанесем линии переключения, соответствующие заданной нелинейной характеристике (рис. 3.10): х = b при y > 0, x = — b при y < 0. Это будут полупрямые П0 и П1 (рис. 3.11).
Рис.3.11
Пусть в точке Q будет t = 0, а в точке Q1 обозначим 
. На участке фазовой траектории QQ1 имеем F(x) = с. Поэтому уравнения (3.17) принимают вид
Интегрирование их дает
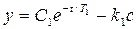(3.18)
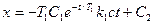(3.19)
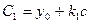
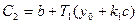
t = τ, х = — b, у = у1
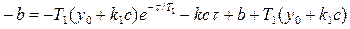
Из последнего уравнения непосредственно находим
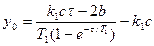(3.21)
Тогда из (3.20) с учетом (3.21) получим
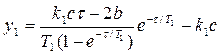(3.22)
Формулы (3.21) и (3.22) и являются искомым законом точечного преобразования в параметрической форме.
Построим диаграмму (рис. 3.12) точечного преобразования в виде кривых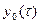 
и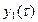 
.
Рис. 3.12.
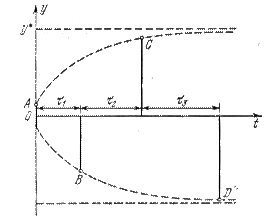
Рис. 3.13.
Рис.3.14
Рис. 3.15.
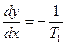
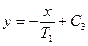(3.23)
Рис.3.16 Рис.3.17
Начнем с первого случая (QQ1Q2). На участке QQ1, где F(x) = с, имеем решения уравнений (3.17) в виде
, 
(3.24)
t = 0, х = b2, у = y0
C1 = y0 + k1c C2 = b2 + T1(y0 + k1c)
В точке Q1 имеем: t = τ 1, x =b1, у = у1
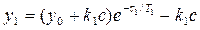
откуда находим
(3.25)
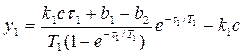(3.26)
Используем далее уравнение (3.23) для участка траектории Q1Q2. С учетом начальных условий
t = τ 1, x = b, y = y1 (3.27)
найдем произвольную постоянную
(3.28)
В точке Q2 имеем t = τ, х = - b2, у = y2. Поэтому из (3.23) получаем
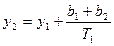(3.29)
или, согласно (3.26),
(3.30)
Рис.3.18
Чтобы определить время для всей траектории QQ1Q2, решим первое уравнение (3.17) на участке Q1Q2, где F(x) = 0. Получим
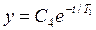
Из начальных условий (3.27)
Откуда
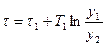
Или, согласно (3.29)
(3.31)
|
|