Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Метод точечного преобразования

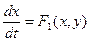
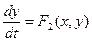(3.12)

Зависимость (3.13),

соответствующая ходу фазовой траектории в силу реше­ния уравнений (3.12), называется функцией последова­ния. Функция последования определяет закон точечного преобразования для данной нелинейной системы.

Рис.3.5.

Определение последующих точек по заданным исход­ным на отрезке АВ и называется точечным преобразова­нием отрезка АВ самого в себя. Ввиду непрерывности расположения фазовых траекторий исходные и последую­щие точки заполняют весь отрезок. Однако каждая точка отрезка АВ не обязательно имеет последующую внутри этого отрезка. Фазовые траектории, пересекающие отре­зок, могут и не возвращаться к нему.

Возможен такой случай, что последующая точка Q' совпадает с исходной Q, т. е.

(3.14)

Рис.3.6

условие устойчивости предельного цикла имеет вид

(3.15)

На других гра­фиках рис. 3.7 показаны: б) случай двух предельных циклов, из которых один неустойчивый, а второй устой­чивый;

Рис.3.7

в) случай расходящихся колебаний; г) случай затухающих колебаний.

Такого типа графики (рис. 3.6, 3.7) называются ди­аграммами точечного преобразования.

В большинстве случаев бывает легче представить функцию последования в параметрической форме.

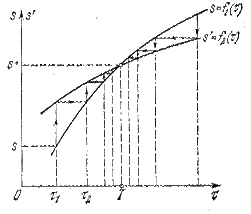
Рис. 3.8

Параметрическая фор­ма точечного преобра­зования в качестве параметра содержит вре­мя прохождения изо­бражающей точки по фазовой траектории от исходной точки Q (рис. 3.5) до ее после­дующей Q'. Через этот параметр на основа­нии решения урав­нений (3.12) выражаются координаты точек Q и Q', а именно

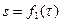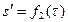, (3.16)

Весь ход точечного преобразования показан на рис. 3.8 стрелками.

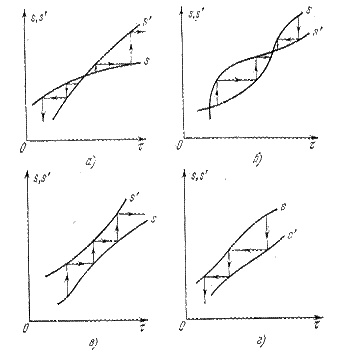
Рис. 3.9.

Рис. 3.9 иллюстрирует параметрические диаграммы точечного преобразования для тех же четырех случаев, что и на рис. 3.7.