Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Построение канонического базиса в общем случае

Линейное пространство является прямой суммой корневых подпространств, если характеристический многочлен линейного оператора 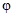разлагается на линейные множители над основным полем К. Поэтому достаточно построить канонический базис каждого корневого подпространства и их объединение – это канонический базис линейного пространства.

Пример. Матрица линейного оператора А в базисе 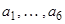линейного пространства имеет вид:

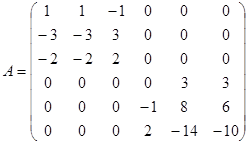
Построить канонический базис.

В этом примере мы будем записывать координаты вектора не в виде матрицы-строки, а в виде матрицы-столбца. Это сделано в связи с тем, что во многих учебниках применяется такая запись и студентам неизбежно придется осваивать обе формы записи. Характеристический многочлен линейного оператора

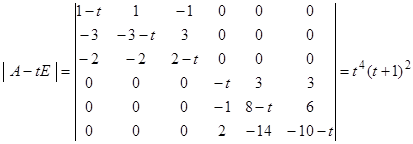
целиком раскладывается на линейные множители. Его корни l₁ = 0, l₂ = -1.

Линейное пространство L можно представить в виде прямой суммы корневых подпространств

L = N ₀Å N _-1 ,, где N ₀ = Ker A ⁴, N _-1 = Ker(A + e).

Построим канонический базис подпространства N ₀. Для этого прежде всего найдем базисы подпространств M_i = Ker (A -0e) ⁱ из возрастающей цепочки

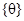= M ₀ Í M ₁ Í M ₂ Í M₃ Í M ₄= N ₀.

В этой цепочке вначале идут строгие включения, а затем равенства. Найдем абсолютный базис M ₁ = Ker A.

Вектор х Î Ker A Û A (x)= qÛ AX = q, где X = (x ₁ x ₂ x ₃ x ₄ x ₅ x ₆ ) ^T – матрица-столбец координат вектора х. Значок Т указывает на то, что необходимо матрицу транспонировать.

Запишем и решим систему AX = q.

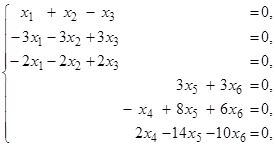
Прибавим ко второму уравнению первое, домноженное на 3, к третьему первое, домноженное на 2. Обе части четвертого уравнения разделим на 3. К шестому уравнению прибавим пятое, домноженное на 2. Новое шестое уравнение совпало с четвертым. Обе части пятого уравнения домножим на –1. Система преобразовалась к следующему виду:

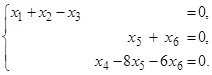
Объявим базисными переменными х ₁, х ₄, х ₆, а свободными х ₂, х ₃, х ₅. Тогда

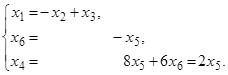
Решение системы

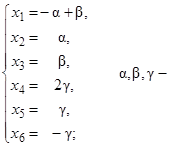любые числа;

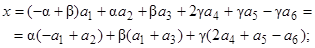
Rang A =3, dim M ₁ =6 –3 =3.Базис М ₁: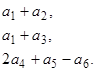

Найдем базис M ₂ = Ker A ².

Вектор х Î Ker A ²Û A ² (x) = q Û A ² X = q, где X = (x ₁ x ₂ x ₃ x ₄ x ₅ x ₆)^T – матрица-столбец координат вектора х.

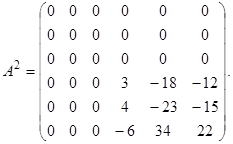
Запишем и решим систему A ² X = q,

~ ~ .

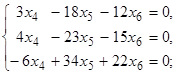
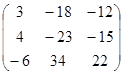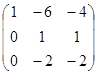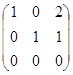Система преобразовалась к виду

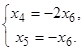
Решение системы 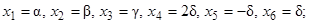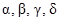– любые числа;

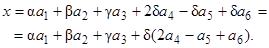
rang A ²=2, dimM ₂= 6 –2 = 4.

Базис М ₂: а ₁, а ₂, а ₃, 2 а ₄– а ₅+ а ₆.

rang A ³ =2, dimM ₃ = 4 Þ М ₂ = М ₃= N ₀.

{q} Ì М ₁ Ì М ₂= N ₀. dimM ₁ = 3, dimM ₂= 4.

Базис М ₁ достроим до базиса М ₂.Добавим к базису М ₁вектор а ₁. Ранг матрицы

составленной из коэффициентов векторов а ₁, - а ₁+ а ₂, а ₁ +а ₃, 2 а ₄+ а ₅ – а ₆, равен 4.Следовательно, эти четыре вектора – базис М ₂. Базис М ₂получен из базиса М ₁ добавлением вектора а ₁, т.е. а ₁ – базис М ₂относительно М ₁. Вектор А (а ₁) = а ₁ –3 а ₂–2 а ₃Î М ₁ можно включить в базис М ₁ вместо вектора – а ₁ +а ₂.

Так как векторы а ₁–3 а ₂ –2 а ₃, а ₁+ а ₃, 2 а ₄+ а ₅ – а ₆ линейно независимы – ранг матрицы из их коэффициентов равен трем:

Канонический базис N ₀: e ₁ = a ₁,

е ₂ = A (a ₁),

е ₃ = a ₂ – a ₁,

е ₄ = 2 a ₄ + a ₅ = a ₆.

Построим канонический базис подпространства N -₁. Найдем базисы подпространств M _i= Ker B ⁱиз возрастающей цепочки

{q}= M ₀ Í M ₁Í M ₂= N _-1; B =(A +e).

Найдем абсолютный базис M₁ = Ker B. Вектор хÎ Ker B Û

Û B(x) = q Û BX = q, где X = (x ₁ x ₂ x ₃ x ₄ x ₅ x ₆ ) ^T – матрица-столбец координат вектора х. Запишем и решим систему BX = q,

B =

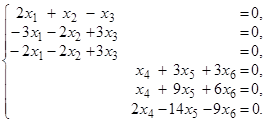
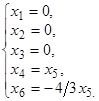
Решение системы: х ₁ = 0,

х ₂ = 0,

х ₃ = 0,

х ₄ = 3 ,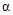

х ₅ = 3 ,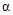

х ₆ = -4 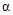, a – любое число.

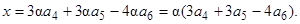
Вектор 3 а ₄+ 3 а ₅ -4 а ₆ – базис М ₁.

Найдем абсолютный базис M ₂= KerB ².Вектор х Î KerB ² Û B ²(x)= q Û B ² X = q, где X = (x ₁ x ₂ x ₃ x ₄ x ₅ x ₆)^T – матрица -столбец координат вектора х. Запишем и решим систему B ² X = q,

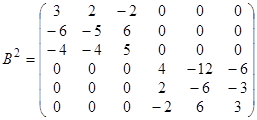
rang B ²= 4, dim M ₂= 6 –4 = 2,

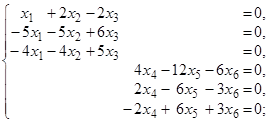
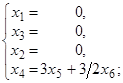
Решение системы: х ₁= 0,

х ₂= 0,

х ₃= 0,

х ₄= 3a +3b,

х ₅ = a,

х ₆ = 2b; a, b – любые числа;

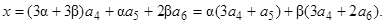
Векторы 3 а ₄ + а ₅, 3 а ₄ +2 а ₆ – базис М₂.

Так как кратность корня –1 равна двум, то {q} = M ₀Ì M ₁Ì M ₂ = N _-1.

Найдем относительный базис M ₁ относительно M ₂. Так как ранг матрицы, составленной из координат векторов 3 а ₄ + 3 а ₅ - 4 а ₆, 3 а ₄ + 2 а ₆, равен двум, то эти векторы линейно независимы в М ₂, и мы заменим полученный базис на новый базис, состоящий из этих элементов. Следовательно, f ₁ =3 а ₄+2 a ₆ – базис M ₁относительно M ₂.Векторы f ₁и В (f ₁) – базис башни.

е ₁ = а ₁, B (e ₁) а ₁ –3 а ₂ –2 а ₃,

e ₂ = а ₂ - а ₁,

e ₃ = -2 а ₄ – а ₅ + а ₆,

f ₁ = 3 а ₄ +2 а ₆,

B (f ₁) = 9 а ₄ +9 а ₅ –12 а ₆ – канонический базис.

Матрица линейного оператора в этом базисе

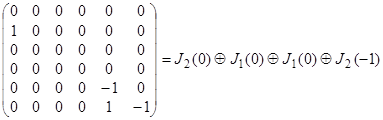
состоит из четырех клеток Жордана, две клетки второго порядка и две – первого.