Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Единственность канонической формы Жордана

Теорема. Матрицы линейного оператора в двух разных канонических базисах составлены из одних и тех же клеток и отличаются лишь порядком расположения клеток.

Доказательство. Возьмем два канонических базиса линейного пространства для линейного оператора j. Суммы порядков клеток Жордана матрицы линейного оператора для его фиксированного собственного значения равны кратности этого собственного значения как корня характеристического многочлена линейного оператора.

Поэтому она одна и та же для матриц линейного оператора в разных канонических базисах (так как матрицы линейного оператора в разных базисах подобны, характеристические многочлены подобных матриц равны и многочлены представляются в виде произведения неприводимых множителей единственным образом). Тем самым доказательство теоремы сводится к доказательству утверждения в корневом пространстве.

Фиксируем произвольное собственное значение 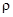линейного оператора и пусть корневое пространство представимо в виде прямой суммы циклических подпространств двумя способами

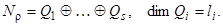
Нам надо доказать, что r = s, k_i = l_i. Без ограничения общности можно считать, что k ₁ ³ k ₂³... ³ k_s, l ₁³ l ₂ ³... ³ l_r. Предположим, что k ₁= l ₁,..., , k_j > l_j; .Тогда

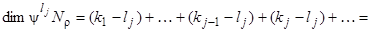
= (l ₁ – l_j) +... + (l_{j -1} – l_j) = k ₁ – l_{j ) +... +} (k_{j –1} – l_j)

(так как k ₁ = l ₁,..., k_j –₁ = l_j –₁) Þ (k_j – l_j) +... = 0.

В сумме (k_j – l_j) +... все слагаемые или равны нулю или положительны. Получили противоречие с тем, что она должна равняться нулю. Продолжив рассуждения аналогичным образом, получим k_i = l_i, r = s.