Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

I.4. Влияние температуры на скорость реакций

В большинстве случаев повышение температуры приводит к увеличению скорости (и константы скорости) химической реакции. Аномальная зависимость константы скорости реакции от температуры наблюдается в некоторых реакциях третьего порядка, ферментативных и цепных реакциях:

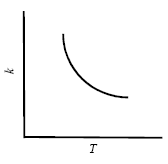
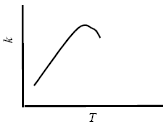
Скорость увеличивается, т.к. при этом возрастает энергия сталкивающихся частиц и повышается вероятность того, что при столкновении произойдет химическое превращение. Для количественного описания температурных эффектов в химической кинетике используют два основных соотношения - правило Вант-Гоффа и уравнение Аррениуса.

Правило Я. Вант-Гоффа: при увеличении температуры на 10⁰С скорость гомогенной реакции возрастает в 2-4 раза:

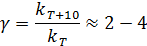
Величина γ - температурный коэффициент скорости (безразмерная величина) показывает, во сколько раз изменяется константа скорости при увеличении температуры на 10 градусов.

Константа скорости зависит от температуры:

Правило Вант-Гоффа получено эмпирически и является приближенным. Значения температурного коэффициента не остаются постоянными при изменении температуры и стремятся к единице при высоких температурах. Поэтому правило можно использовать для полуколичественных оценок в области сравнительно низких температур. Более точно зависимость константы скорости от температуры передается уравнением Аррениуса

Уравнение С. Аррениуса:

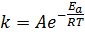
или в логарифмических координатах (рис. 4):

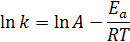
А – предэкспоненциальный множитель, который не зависит от температуры и определяется типом реакции. Физический смысл А в случае простых реакций: мономолекулярных - это частота колебаний по разрываемой связи (А» 10¹³ сек^-1), бимолекулярных - величина А пропорциональна общему числу столкновений между молекулами реагирующих веществ (А» 10^-10 ¸ 10^-11 см³/(молекул·сек).

Е_а - энергия активации химической реакции (кДж/моль) также не зависит от температуры. В случае простых реакций показывает, какой минимальной (избыточной по сравнению со средней) энергией в расчете на 1 моль должны обладать реагирующие частицы, чтобы они могли вступить в химическую реакцию. В случае сложных реакций называется эмпирической или кажущейся энергией активации и в общем случае зависит от энергий активации отдельных стадий данной реакции.

Для большинства реакций в растворе Е_а составляет 50 – 100 кДж/моль, реакции между валентнонасыщенными молекулами в газовой фазе характеризуются значениями 100 - 200 кДж/моль. Для реакций с участием активных частиц (свободные атомы, радикалы) энергия активации может составлять 0 – 10 кДж/моль.

Графическая зависимость константы скорости реакции от температуры представлена на рисунке.

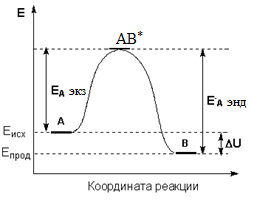
При выводе уравнения Аррениус предположил, что реагировать (превращаться в продукты) могут не все молекулы, а лишь некоторые из них, находящиеся в особом активном состоянии. Эти молекулы образуются из обычных в эндотермическом процессе с поглощением энергии E_A и роль температуры сводится к смещению равновесия в ту или иную сторону на этой стадии. Так, например, в реакции

A ® продукты

активные молекулы А* образуются из молекул А по схеме:

A ↔ A*

По Аррениусу, этот процесс является обратимым и быстрым, так что в системе всегда сохраняется термодинамическое равновесие между А и А*, которое можно характеризовать константой равновесия K_c:

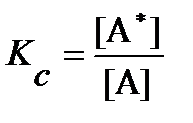или [A*] = K_c[A].

Превращение активных молекул в конечный продукт осуществляется со скоростью, не зависящей от температуры и относительно медленно:

[A*] ® B

Таким образом, скорость реакции равна (принцип лимитирующей стадии):

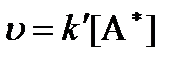
где k’ – константа скорости реакции (медленной стадии), не зависящая от температуры.

Подставляя величину концентрации активных молекул из выражения для термодинамической константы равновесия можно получить:

.

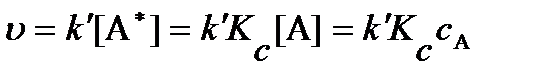Так как k’ не зависит от температуры, то температурная зависимость константы скорости определяется уравнением изохоры Вант-Гоффа для константы равновесия:

.

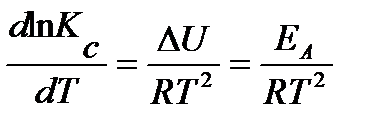Интегрируя уравнение в предположении независимости энергии активации от температуры, получим выражение, совпадающее с эмпирическим уравнением Аррениуса:

,

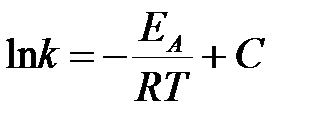где С – константа интегрирования.

Потенцируя уравнение, можно представить его в экспоненциальной форме, полагая e^C = A:

.

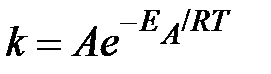Для обратимой реакции:

k₁

А ↔ В

k_-1

разность энергий активации прямой и обратной реакций равна тепловому эффекту прямой реакции:

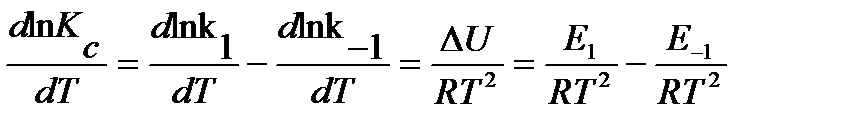
Энергию активации можно определить как аналитически по уравнению:

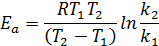
так и графическим методом. Для этого необходимо знать ряд констант скоростей при разных температурах. Если реакция подчиняется уравнению Аррениуса, то зависимость ln k от 1/ T должна выражаться прямой линией:

Рис. 5. Зависимость ln k от 1/T

Расчет по методу равных выходов (метод полупревращений) не требует знания констант. Если условия процесса (C_{0, A}, α) при различных температурах одинаковы, то уравнение любого порядка реакции можно представить в виде:

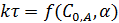
Так как правые части одинаковы, можно записать:

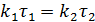
Таким образом, отношение констант можно заменить обратным отношением соответствующих времен:

Связь между энергией активации и температурным коэффициентом:

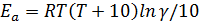
Чем больше энергия активации, тем меньше константа скорости, но тем быстрее она увеличивается с ростом температуры (больше значение температурного коэффициента).