Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
I.3. Методы определения порядка реакций.
|
|
Методы определения порядка реакции делятся на две группы (интегральные и дифференциальные) в зависимости от того, какой вид кинетического уравнения они используют. Каждый из методов, в свою очередь, может быть осуществлен численно (аналитически) и графически.
Интегральные методы: метод подстановки, метод Оствальда – Нойеса и метод полупревращения.
Метод подстановки заключается в том, что экспериментальные результаты (текущие концентрации веществ в моменты времени) последовательно подставляются в интегральные кинетические уравнения реакций различных порядков и определяется, какое из уравнений дает практически постоянную величину константы скорости. Именно это уравнение и определяет порядок исследуемой реакции. В графическом варианте строятся графики, выражающие зависимости различных функций концентрации от времени, и определяется, для какой из них наблюдается прямолинейная зависимость. Это уравнение и определяет порядок исследуемой реакции.
Рис. 5. Линейные зависимости различных функций концентрации реагирующего вещества от времени
Определение порядка реакции методом Оствальда-Нойеса основано на использовании зависимости периода превращения исходного вещества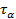 
на определенную долю α от начальной концентрации. Из кинетического уравнения реакции n- го порядка можно получить отношение двух периодов 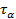для двух начальных концентраций:
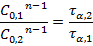
После логарифмирования:
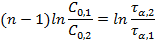
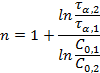
Метод полупревращения – является частным случаем метода Оствальда-Нойеса для условия α =1/2. Более точно этим методом можно определить порядок реакции графически, если известны несколько значений τ 1/2 при нескольких начальных концентрациях. Логарифмируя выражение для периода полупревращения реакции n-го порядка можно получить:
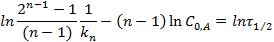
При построении графика по оси ординат откладываются значения ln(τ 1/2), а по оси абсцисс - значения ln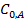 
, тогда n = 1–tga.
Дифференциальные методы. Определение порядка реакции методом Вант-Гоффа основано на использовании основного постулата химической кинетики в дифференциальной форме:
Для двух значений скорости реакции при двух концентрациях:
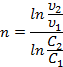
В графическом варианте порядок реакции определяют по тангенсу угла наклона прямой в логарифмических координатах скорости от концентрации.
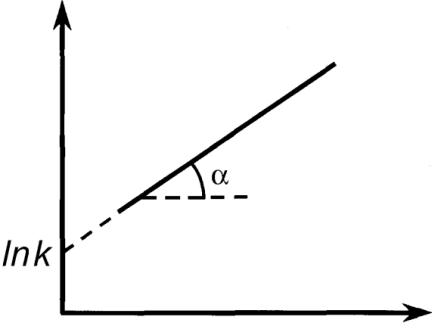
Истинные скорости реакции можно найти или графическим дифференцированием кинетических кривых (т.е. зависимостей концентраций реагирующих веществ от времени) – метод касательных – или заменив их на средние скорости.
Определение скорости реакции по кинетическим кривым методом касательных
Определение частного порядка реакции проводят методом изолирования Оствальда (метод понижения порядка реакции).
Если в исследуемой реакции исходных реагирующих веществ более одного (например, три - А, В, С), то сначала определяют порядок реакции одним из указанных выше методов по одному из веществ (А), взяв остальные вещества (В и С) в большом избытке, затем определяют порядок реакции по веществу В, взяв А и С в большом избытке, и т.д. Так, в случае реакции А + В + С ® D ее скорость в общем случае равна
.
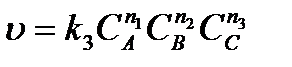Если вещества В и С взяты в большом избытке, то при протекании реакции их концентрации практически не изменяются, т.е.
.
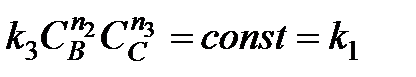Тогда
.
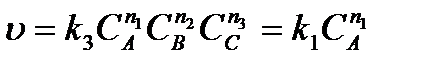Определив порядки реакции по каждому из реагирующих веществ, можно найти общий порядок реакции: n = n 1 + n 2 + n 3.
|
|