Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сложение и вычитание

В ОПУ операции сложения и вычитания являются более сложными, чем операции умножения и деления.

Включают в себя этапы:

1. Подготовительный;

2. Далее производится проверка с целью выяснения, не равен ли нулю один из операндов. Если это имеет место, в качестве результата сразу берется другой операнд.

3. Определяется операнд, имеющий меньший порядок. В нем производится сдвиг мантиссы вправо на число разрядов, равное разности порядков операндов. Например, .

Выравнивания порядков можно достичь сдвигом мантиссы меньшего из чисел вправо, с одновременным увеличением порядка этого числа, либо сдвигом мантиссы большего из чисел влево и уменьшением его порядка. Оба варианта сопряжены с потерей цифр мантиссы, но выгоднее сдвигать меньшее из чисел, так как при этом теряются младшие разряды мантиссы. Таким образом, выравнивание порядков операндов реализуется путем сдвига мантиссы меньшего из чисел на один разряд вправо с одновременным увеличением порядка этого числа на единицу. Действия повторяются до совпадения порядков. Если в процессе сдвига мантисса обращается в 0, в качестве результата операции берется другой операнд.

4. приравнивание порядка результата большему из порядков операндов.

5. сложение и вычитание мантисс и определение знака результата.

6. проверка на переполнение.

При одинаковых знаках мантисс может произойти переполнение. В этом случае мантисса результата сдвигается вправо на один разряд, а порядок результата увеличивается на единицу. Если при этом происходит переполнение поля порядка, то операция прекращается и формируется признак переполнения, сопровождаемый соответствующим предупреждением (обычно в виде сигнала прерывания);

7. заключительный этап.

Сложение и вычитание выполняются идентично, но в случае вычитания необходимо изменить знак второго операнда на противоположный.

В отличие от целочисленной арифметики, в операциях с ПЗ сложение и вычитание производятся приближенно, так как при выравнивании порядков происходит потеря младших разрядов одного из слагаемых. В этом случае погрешность всегда отрицательна и может доходить до единицы младшего разряда.

Потеря значимости может произойти при:

- сложении и вычитании мантиссы;

- сдвиге мантиссы вправо для устранения переполнения;

- сдвиге мантиссы влево (до тех, пор пока старшую позицию не займет единица);

- порядок может стать отрицательным (в ходе сдвига мантиссы уменьшается порядок: получение отрицательного значения свидетельствует о получении числа, непредставимого в данном формате, так как значения смещенных порядков всегда положительны).

Алгоритм сложения нормализованных чисел представлен в виде блок-схемы на Рис.1.1.

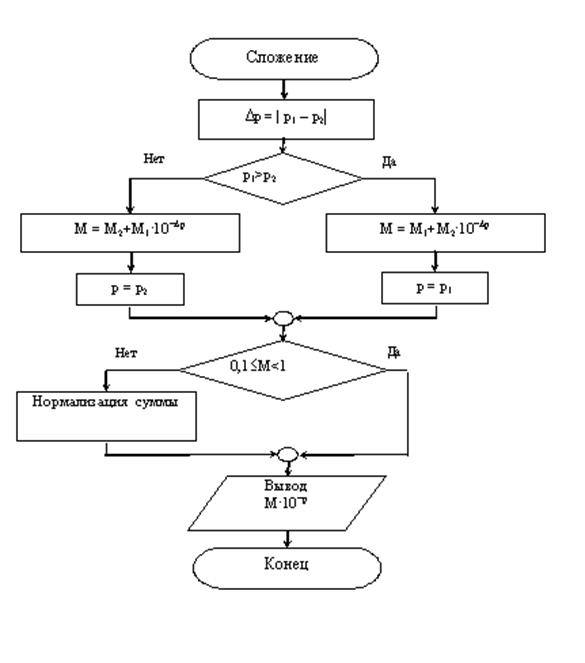
Рисунок -Блок-схема алгоритма сложения нормализованных чисел

Например, X₁=0, 87654× 10¹, а X₂=0, 94567× 10². Согласно алгоритму Dp=1 и p₁< p₂. Следовательно, p=p₂=2, а мантисса числа X₁ должна быть сдвинута на 1 разряд вправо (при этом из-за ограниченности разрядно сетки пропадет цифра 4). Новая мантисса получается суммированием: M=0, 94567+0, 08765=1, 03332; поскольку она выходит за допустимый интервал представления мантисс, необходимо его нормализовать M’=0, 10333 (при этом теряется цифра 2 в меньшем разряде); p’=p+1=3. Окончательно получаем: X=0, 10333× 10³. Точный результат суммирования оказался бы 103, 3324. Таким образом, сложение чисел в нормализованной форме с ограниченной длиной разрядной сетки приводит к появлению погрешностей операции сложения. Более того, можно показать на примерах (рекомендуется это сделать самостоятельно), что такое суммирование не обладает ассоциативностью, т.е. (X₁Å X₂)Å X₃¹ X₁Å (X₂Å X₃).