Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
Особенности умножения при различных сочетаниях знаков сомножителей.
|
|
При выполнении операции арифметического сдвига вправо для суммы частичных произведений – освободившиеся при сдвиге цифровые позиции должны заполняться не нулем, а значением знакового разряда сдвигаемого числа.
Это правило начинает действовать лишь с момента, когда среди анализируемых разрядов множителя появляется первая единица.
| Множимое – отрицательное, (A< 0), множитель – положительный (B> =0) |
|
Множимое произвольного знака, множитель положительный.
В данном случае требуется коррекция результата.
Так как множитель отрицателен, он записывается в дополнительном коде [B]Д=2n-|B|, и в цифровых разрядах кода будет представлено число 2 n-1 - |B|. При типовом умножении (как в случае B> =0) получим 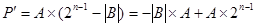 . Псевдопроизведение Р больше истинного произведения Р на величину Ах2 n-1, что и необходимо учитывать при формировании окончательного результата. Для этого перед последним сдвигом из полученного псевдопроизведения необходимо вычесть избыточный член.
|
| Множимое – положительное (A> =0), множитель – отрицательный (B< 0) |
|
| Множимое – отрицательное (A< 0), множитель – отрицательный (B< 0) |
|
Сравнение алгоритмов сдвига влево и вправо
| Преимущества | Недостатки | |
| Алгоритм сдвига вправо | Для реализации алгоритма требуется n-разрядный сумматор. | Требует дополнительных затрат оборудования на реализацию цепей сдвига в сумматоре. |
| Алгоритм сдвига влево | Позволяет совмещать во времени операции сложения и сдвига. | Для реализации алгоритма требуется 2* n-разрядный сумматор (дополнительных затрат оборудования на реализацию дополнительных разрядов сумматора) Неудобен при выполнении умножения над числами с разными знаками. |
|
|