Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Алгоритм Бута

В основе алгоритма Бута лежит следующее соотношение, характерное для последовательностей двоичных цифр:

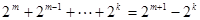, где m и k - номера крайних разрядов в группе из последовательностей единиц.

Например 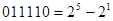. Это означает, что при наличии в множителе групп из нескольких единиц (комбинаций вида 011, 110), последовательное добавление к СЧП множимого с нарастающим весом от (2^k до 2^m) можно заменить вычитанием из СЧП множимого с весом 2^k и прибавлением множимого с весом 2^m+1.

Алгоритм предполагает выполнение трех операций: сдвиг, сложение и вычитание.

Помимо сокращения числа сложений у него есть еще одно достоинство – он в равной степени применим к числам без знака и со знаком.

Алгоритм Бута сводится к перекодированию множителя из системы (0, 1) в избыточную систему (-1, 0, 1), из-за чего его часто называют перекодированием Бута:

1 –означает добавление множимого к сумме частичных произведений (СЧП);

-1 – вычитание множимого;

0 –не предполагает никаких действий.

Реализация алгоритма предполагает последовательный справа налево анализ пар разрядов множителя b_ib_i-1 (для i=0 b_i-1считается равным 0).

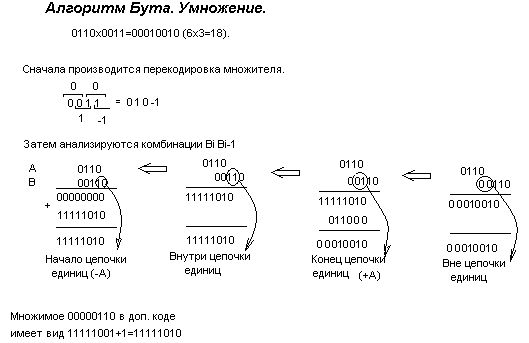
Деление для компьютера является трудной операцией. Обычно оно реализуется путем многократного прибавления к делимому дополнительного кода делителя.
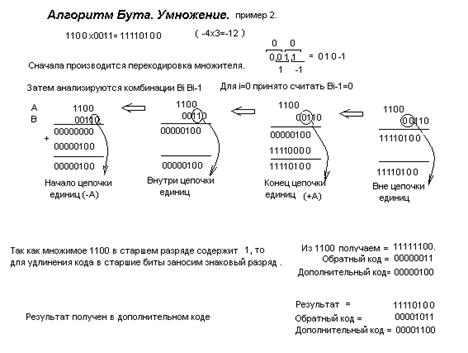