Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Выполнение корреляционно-регрессионного анализа с помощью компьютера

Корреляционно-регрессионный анализ можно осуществить, использую табличный процессор Excel или программный комплекс Statistica. Поскольку Excel находит более широкое применение, то будем работать именно с ним. Следует уточнить, что в Excel линии регрессии называются линиями тренда.

Анализ осуществляем в следующей последовательности:

1) создаем новую книгу Excel. Вводим заголовок зависимости и исходные данные, приведенные в таблице 1;

2) создаем (с помощью Мастера диаграмм) поле корреляции – диаграмму рассеяния или разброса;

3) на поле корреляции наносим возможные линии регрессии (линии тренда). Для этого, открыв контекстное меню на поле корреляции, выбираем команду «Добавить линию тренда». При этом в диалоговом окне на вкладке «Тип» будут показаны возможные типы линий тренда. Поочередно наносим их на поле корреляции, в т.ч.: линейную (рисунок 4), логарифмическую (рисунок 5), полиноминальную (рисунок 6), степенную (рисунок 7), экспоненциальную (рисунок 8).

При этом каждый раз на вкладке «Параметры» задаем размещение уравнения и значение достоверности аппроксимации (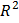). Полученные результаты сводим в таблицу 7.

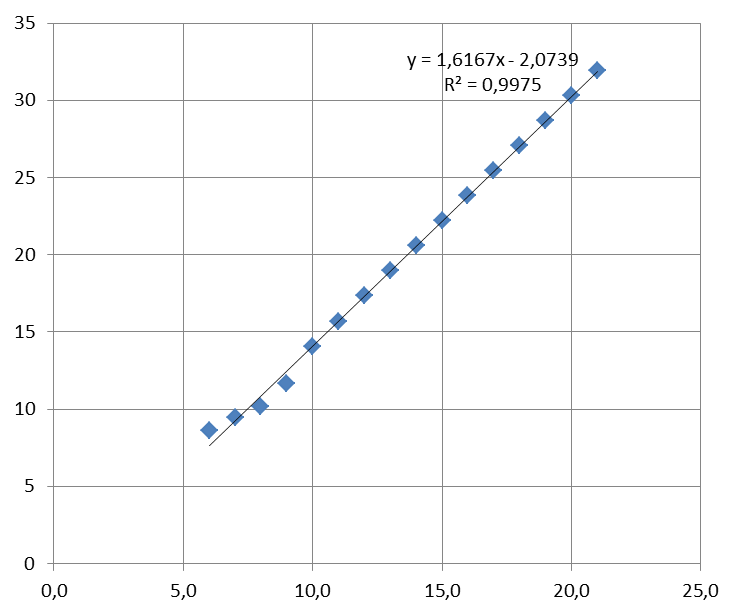
Рисунок 4 – Линейная линия тренда

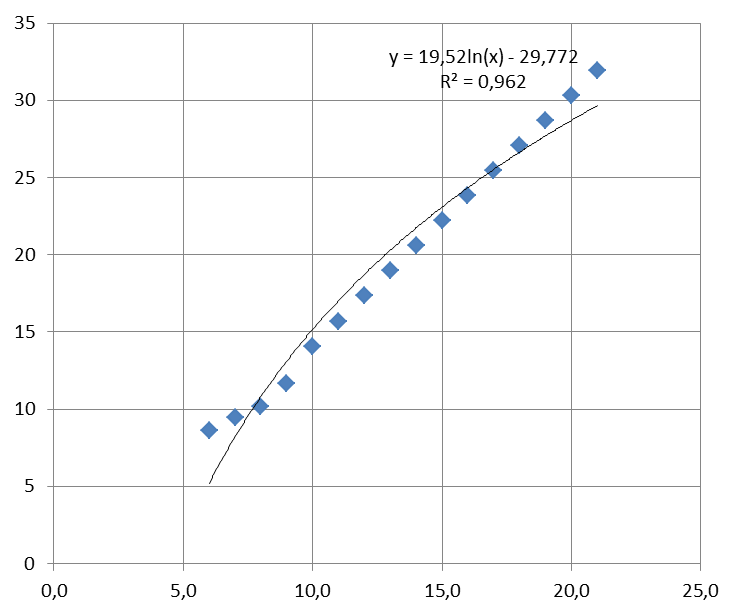
Рисунок 5 – Логарифмическая линия тренда

Рисунок 6 – Полиноминальная линия тренда

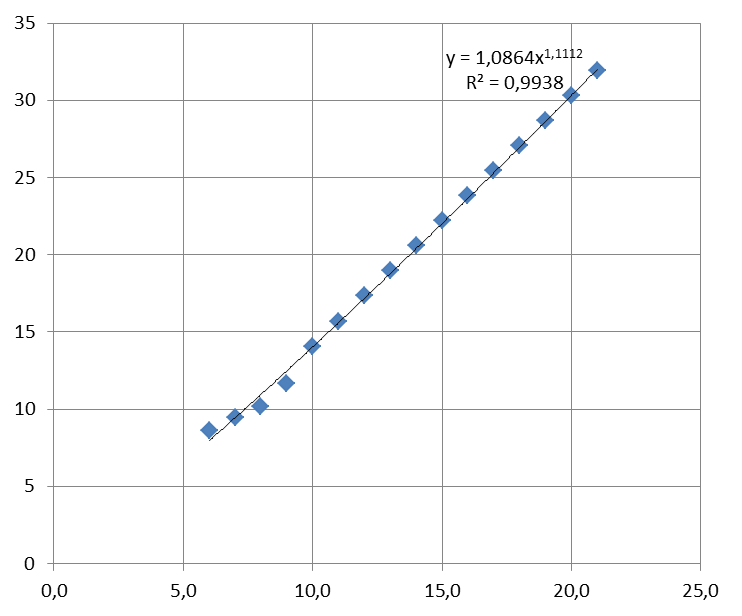
Рисунок 7 – Степенная линия тренда

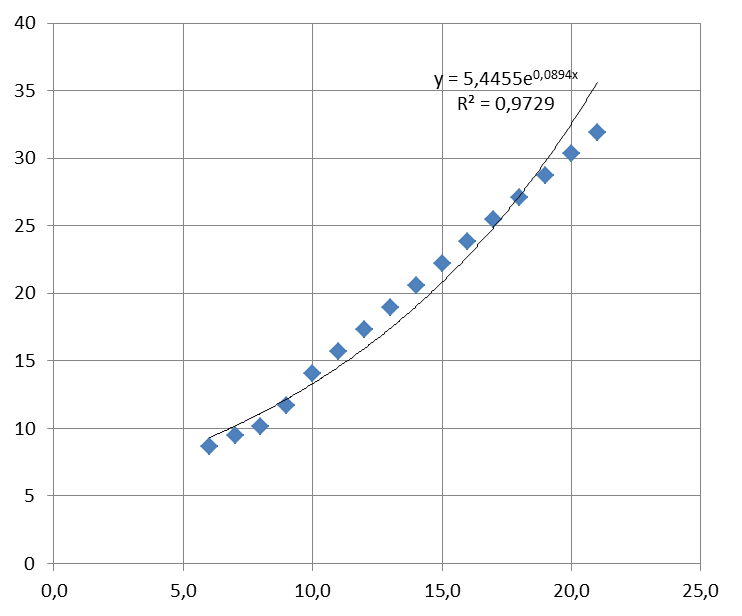
Рисунок 8 – Экспоненциальная линия тренда

Таблица 7 - Сравнение полученных уравнений регрессии

Уравнение		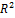Вывод
y = 1, 616x - 2, 073	0, 997	Да
y = 19, 52ln(x) - 29, 77	0, 962	Нет
y = 0, 006x2 + 1, 449x - 1, 075	0, 997	Да
y = 1, 086x1, 111	0, 993	Нет
y = 5, 445e0, 089x	0, 972	Нет

4) Находим линию тренда, имеющую наибольшее значение достоверности аппроксимации – линейную (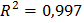), которую и выбираем в качестве линии парной регрессии для исследуемой зависимости.