Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение коэффициента корреляции (корреляционного отношения) и средней относительной ошибки аппроксимации
|
|
Теснота связи между двумя параметрами характеризуется коэффициентом корреляции (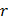
) для линейных зависимостей и корреляционным отношением (
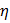) для нелинейных; дополнительной оценкой точности аппроксимации является средняя относительная ошибка аппроксимации (
).
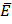Данные параметры определяем для рассмотренных видов регрессии:
а) парной линейной
%
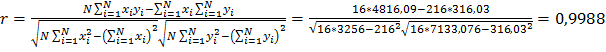
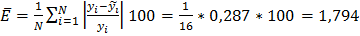б) парной логарифмической
%
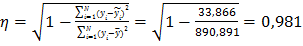
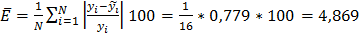в) парной степенной
%
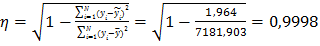
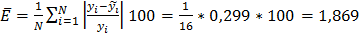Полученные результаты сравниваем между собой, используя таблицу 5.
Таблица 5 – Сравнение полученных уравнений регрессии
| Уравнение регрессии |  ( )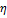
|  , %
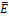| Вывод |
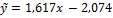
| 0, 9988 | 1, 794 | Да |
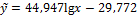
| 0, 981 | 4, 869 | Нет |
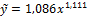
| 0, 9998 | 1, 869 | Нет |
По данным таблицы 5 можно сделать вывод о том, что наилучшей аппроксимацией (по 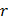(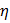) и 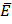) для рассматриваемого примера обладает парная линейная регрессия. Поэтому именно для нее будем вести дальнейший анализ.
|
|