Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Умножение матрицы на число и сложение матриц

По определению, чтобы умножить матрицу на число , нужно каждый элемент матрицы умножить на это число.

Пример 1. Умножить матрицу на число

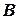Складывать можно только матрицы с одинаковым числом строк и столбцов. Суммой матриц и называется матрица , элементы которой равны суммам соответствующих элементов матриц и : .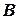

Пример 2. Сумма двух матриц

.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается через . Для любой матрицы имеем , .

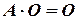Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:

1) ,

2) ,

3) ,

4) ,

5) .

где , , 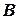- матрицы, , - числа.

Произведение матриц

Произведение матрицы на матрицу 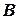определено только в том случае, когда число столбцов матрицы равно числу строк матрицы 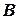. В результате умножения получим матрицу , у которой столько же строк, как у матрицы , и столько же столбцов, как у матрицы .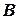

По определению элемент 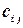матрицы равен сумме парных произведений элементов 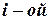строки матрицы , на соответствующие элементы столбца матрицы .

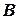Пример 3. Найти произведение матриц

и .

Решение. Имеем: матрица размера 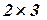, матрица 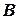размера , тогда произведение существует и элементы матрицы равны

, , ,

, .

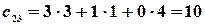, а произведение не существует.

Пример 4. Найти произведение матриц

,

Очевидно, что произведение матриц не обладает перестановочным свойством, т.е. некоммутативно. Если все-таки выполняется равенство , то матрицы и 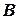называются перестановочными.

Свойства произведения матриц:

1) , где -число;

2) ;

3) ;

4) .

Единичной матрицей называется диагональная матрица, у которой все элементы равны 1.

.

Свойство единичной матрицы: для любой квадратной матрицы .

Рассмотрим произвольную квадратную матрицу , порядка 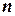. Если существует такая матрица 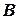, что , то говорят, что обратима, а 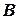называют обратной матрицей для матрицы .

Определитель матрицы

Определителем квадратной матрицы называется число, которое обозначается через или 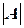и вычисляется при помощи следующих трех правил.

Правило 1. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали.

Замечание: Определитель одноэлементной матрицы равен самому элементу.

Правило 2. Общий множитель элементов любой строки или столбца матрицы можно вынести за знак определителя.

Замечание: Определитель матрицы, у которой строка или столбец состоит только из нулей, равен .

Правило 3. Определитель матрицы не изменится, если к одной из строк (столбцов) матрицы прибавить другую строку (столбец) этой матрицы.