
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Двойственные задачи линейного программирования
|
|
Теоретические положения
Каждой задаче линейного программирования соответствует другая задача, называемая двойственной или сопряженной по отношению к исходной. Теория двойственности используется для проведения качественных исследований задач линейного программирования.
Рассмотрим экономический смысл двойственной задачи. В качестве исходной возьмем задачу, рассмотренную в первой лабораторной работе. Предположим, что некоторая организация решила закупить ресурсы, которыми располагает фирма (см. предыдущую задачу). Необходимо определить оптимальные цены на эти ресурсы. Под оптимальными в данном случае понимают цены, приемлемые как для продавца, так и для покупателя.
Очевидно, что покупающая организация заинтересована в том, чтобы затраты Z на все ресурсы в количествах b  , b
, b  , …, b
, …, b 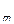 по ценам y
по ценам y  , y
, y  , …, y
, …, y 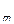 , были минимальны, т.е.
, были минимальны, т.е.
Z = b  y
y  + b
+ b  y
y  +…+ b
+…+ b 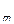 y
y 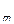
 min.
min.
С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная от продажи выручка была бы не менее выручки от реализации произведенной продукции. На изготовление единицы продукции первого вида расходуется a  ресурса первого вида, a
ресурса первого вида, a  ресурса второго вида, a
ресурса второго вида, a  ресурса m-го вида. Поэтому для удовлетворения интересов продавца выручка то продажи ресурсов, необходимых для производства единицы продукции первого вида, должна быть не меньше ее цены c
ресурса m-го вида. Поэтому для удовлетворения интересов продавца выручка то продажи ресурсов, необходимых для производства единицы продукции первого вида, должна быть не меньше ее цены c  , т.е.
, т.е.
a  y
y  + a
+ a  y
y  + … + a
+ … + a  y
y 
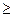 c
c  .
.
Аналогично можно составить неравенства по другим видам продукции.
Экономико-математическая модель и содержательная интерпретация полученной таким образом двойственной задачи приведены в таблице.
Таблица 2
| Задача I (исходная) | Задача II (двойственная) |
F=c  x x  +c +c  x x  +…+c +…+c  x x   max
при ограничениях:
a max
при ограничениях:
a 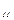 x x  +a +a  x x  …+a …+a  x x   b b  ,
a ,
a  x x  a a  x x  +…+a +…+a 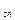 x x   b b  ………………………………………. a
………………………………………. a  x x  +a +a  x x  +…+a +…+a  x x   b b  и условии неотрицательности
x
и условии неотрицательности
x   0 (j=1, 2, …, l; l 0 (j=1, 2, …, l; l  n).
Составить такой план выпуска продукции X=(x n).
Составить такой план выпуска продукции X=(x  , x , x  , …, x , …, x  ), при котором выручка от реализации продукции будет максимальна при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов. ), при котором выручка от реализации продукции будет максимальна при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов.
| Z= b  y y  +b +b  y y  +…+ b +…+ b  y y   min
при ограничениях:
a min
при ограничениях:
a 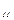 y y  + a + a  y y  +…+ a +…+ a  y y  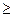 c c  ,
a ,
a  y y  + a + a  y y  +… + a +… + a  y y   c c  ,
…………………………………………….
a ,
…………………………………………….
a  y y  + a + a  y y  +…+ a +…+ a  y y   c c  ,
и условии неотрицательности
y ,
и условии неотрицательности
y   0 (i=1, 2, …, m).
Найти такой набор цен Y = (y 0 (i=1, 2, …, m).
Найти такой набор цен Y = (y  , y , y  , …, y , …, y  ), при которомзатраты покупателя на приобретение ресурсов минимальны, а выручка от продажи ресурсов, идущих на производство продукции каждого вида, будет не менее выручки от реализации этой продукции. ), при которомзатраты покупателя на приобретение ресурсов минимальны, а выручка от продажи ресурсов, идущих на производство продукции каждого вида, будет не менее выручки от реализации этой продукции.
|
Алгоритм составления двойственной задачи.
1. Составить расширенную матрицу системы A  , в которую включить матрицу коэффициентов при переменных системы ограничений, столбец свободных членов системы и строку коэффициентов при переменных в выражении целевой функции.
, в которую включить матрицу коэффициентов при переменных системы ограничений, столбец свободных членов системы и строку коэффициентов при переменных в выражении целевой функции.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
2. Найти матрицу A  , транспонированную к матрице A
, транспонированную к матрице A  .
.
3. Сформулировать двойственную задачу на основе полученной матрицы A  и условия неотрицательности переменных.
и условия неотрицательности переменных.
Пример
Используя в качестве исходной задачу линейного программирования из лабораторных работ № 1, 2, составить двойственную ей задачу и решить симплексным методом.
Условие исходной задачи
Система ограничений:
x  +3x
+3x 

2x  +x
+x 

x 

3x 
 .
.
Дополнительные условия задачи:
x  x
x 
Линейная функция имеет вид:
F=2x 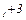 x
x  max.
max.
1. Составим расширенную матрицу системы
A  =
= 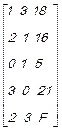 .
.
2. Найдем транспонированную матрицу
A  =
=  .
.
3. Сформулируем двойственную задачу
Z =18 y  + 16 y
+ 16 y  +5y
+5y  + 21 y
+ 21 y 
 min
min
при ограничениях
y  + 2 y
+ 2 y  + 3 y
+ 3 y 
 2,
2,
3 y  + y
+ y  + y
+ y 
 3.
3.
Решение
Введем дополнительные неотрицательные переменные y  и y
и y  со знаком «минус», т.к. неравенства имеют вид «
со знаком «минус», т.к. неравенства имеют вид « ». Получим систему уравнений
». Получим систему уравнений
y  + 2 y
+ 2 y  + 3 y
+ 3 y  - y
- y  = 2,
= 2,
3 y  + y
+ y  + y
+ y  - y
- y  = 3.
= 3.
Если в качестве основных переменных взять как в исходной задаче дополнительные переменные, то получим базисное решение: (0; 0; 0; 0; -2; -3). Наличие отрицательных компонент в решении свидетельствует о его недопустимости. Поэтому следует выбрать набор основных переменных, дающих допустимое решение.
I шаг
Основные переменные: y  , y
, y  .
.
Неосновные переменные: y  , y
, y  , y
, y  , y
, y  .
.
Выражаем основные переменные через неосновные
y  = 3 - 3 y
= 3 - 3 y  - y
- y  + y
+ y  ,
,
y  = (2/3) – (1/3) y
= (2/3) – (1/3) y  - (2/3) y
- (2/3) y  + (1/3) y
+ (1/3) y  .
.
Первое базисное решение Y  = (0; 0; 3; 2/3; 0; 0) является допустимым. Выражаем целевую функцию через неосновные переменные: Z = 18 y
= (0; 0; 3; 2/3; 0; 0) является допустимым. Выражаем целевую функцию через неосновные переменные: Z = 18 y  + 16 y
+ 16 y  + 5 y
+ 5 y  + 21 y
+ 21 y  = 18 y
= 18 y  + 16 y
+ 16 y  + 5(3 - 3 y
+ 5(3 - 3 y  - y
- y  + y
+ y  ) + 21((2/3) – (1/3) y
) + 21((2/3) – (1/3) y  - (2/3) y
- (2/3) y  + (1/3) y
+ (1/3) y  ) = 29 - 4 y
) = 29 - 4 y  - 3 y
- 3 y  + + 7 y
+ + 7 y  + 5 y
+ 5 y  . Коэффициенты при переменных y
. Коэффициенты при переменных y  и y
и y  отрицательны, что свидетельствует о возможности дальнейшего уменьшения значения функции Z. На следующем шаге будем переводить переменную y
отрицательны, что свидетельствует о возможности дальнейшего уменьшения значения функции Z. На следующем шаге будем переводить переменную y  в основные. Для нее наибольшее возможное значение y
в основные. Для нее наибольшее возможное значение y  = min(3/3; 2/3; 1/3) = 1, а первое уравнение является разрешающим.
= min(3/3; 2/3; 1/3) = 1, а первое уравнение является разрешающим.
II шаг
Основные переменные: y  , y
, y  .
.
Неосновные переменные: y  , y
, y  , y
, y  , y
, y  .
.
После преобразований получим
y  = 1 - (1/3) y
= 1 - (1/3) y  - (1/3) y
- (1/3) y  + (1/3) y
+ (1/3) y  ,
,
y  = 1/3 – (5/9) y
= 1/3 – (5/9) y  + (1/9) y
+ (1/9) y  + (1/3) y
+ (1/3) y  - (1/9) y
- (1/9) y  ,
,
Z = 25 – (5/3) y  + (4/3) y
+ (4/3) y  + 7 y
+ 7 y  + (11/3) y
+ (11/3) y  .
.
Переменную y  переводим в основные. Ее наибольшее возможное значение y
переводим в основные. Ее наибольшее возможное значение y  = min (3; 3/5) = 3/5. Второе уравнение является разрешающим, а переменная y
= min (3; 3/5) = 3/5. Второе уравнение является разрешающим, а переменная y  переходит в неосновные.
переходит в неосновные.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
|
|
