
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Геометрический метод решения задачи линейного программирования
|
|
Постановка задачи линейного программирования
Дана система m линейных уравнений и неравенств с n переменными:
a 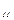 x
x  +a
+a  x
x  …+a
…+a  x
x 
 b
b  ,
,
a  x
x  a
a  x
x  +…+a
+…+a 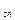 x
x 
 b
b 
……………………………………….
a  x
x  +a
+a  x
x  +…+a
+…+a  x
x 
 b
b 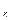 ,
,
a  x
x  +a
+a  x
x  +…+a
+…+a 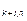 x
x  =b
=b  , (1)
, (1)
a  x
x  +a
+a 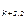 x
x  +…+a
+…+a  x
x  =b
=b 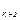 ,
,
………………………………………………….
a  x
x  +a
+a  x
x  +…+a
+…+a  x
x  =b
=b  ,
,
и линейная (целевая) функция
F=c  x
x  +c
+c  x
x  +…+c
+…+c  x
x  . (2)
. (2)
Необходимо найти такое решение системы (1) X=(x  , x
, x  , …, x
, …, x  ,.., x
,.., x  ), где
), где
x 
 0 (j=1, 2, …, l; l
0 (j=1, 2, …, l; l  n), (3)
n), (3)
при котором линейная функция (2) принимает оптимальное (т.е. максимальное или минимальное) значение.
Система (1) называется системой ограничений, а функция F – линейной функцией, линейной формой, целевой функцией или функцией цели.
Оптимальным решением (или оптимальным планом) задачи линейного программирования называется решение X=(x  , x
, x  , …, x
, …, x  ) системы ограничений (1), удовлетворяющее условию (3), при котором линейная функция (2) принимает экстремальное (максимальное или минимальное) значение.
) системы ограничений (1), удовлетворяющее условию (3), при котором линейная функция (2) принимает экстремальное (максимальное или минимальное) значение.
При условии, что m< n, система ограничений (1) имеет множество решений. Решения задачи, удовлетворяющие системе (1) и дополнительным условиям (3), называются допустимыми.
Геометрический метод решения задачи линейного программирования основан на использовании теоремы.
Множество решений совместной системы m линейных неравенств с двумя переменными является выпуклым многоугольником (или выпуклой многоугольной областью). Оптимальное решение задачи линейного программирования располагается в одной из угловых точек многоугольника решений.. Если линейная функция принимает экстремальное значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек, т.е располагается на отрезке, соединяющем точки..
Многоугольник допустимых решений задачи может быть построен геометрическим методом (см. пример решения). Оптимальное решение выбирается либо путем перебора угловых точек, либо с использованием понятия линии уровня. Линией уровня линейной функции F называется линия, вдоль которой эта функция принимает одно и то же фиксированное значение F=a..
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Пример
Решить задачу линейного программирования геометрическим методом.
|
|
