Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
III шаг.
|
|
Таблица поставок:
Таблица 6
 2
|  3
| -2 | ||||||
 1
|  3
 30
| -3 | ||||||
 3
|
 20
| -3 | ||||||
| -3 | ||||||||
 2
|  1
| -3 | ||||||
Матрица оценок свободных клеток:
В =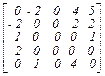 
.
Цикл пересчета для клетки (2, 1):
(1, 1) – + (1, 3)
20 20
 |  | ||
(2, 1) + – (2, 3)
0
Максимально возможная поставка в клетку (2, 1) равна:
x 
= min (20, 0) = 0.
На первый взгляд может показаться, что нулевая поставка в рассматриваемую клетку лишена смысла, т.к. не скажется на значении целевой функции. Однако в симплексном методе значение целевой функции не должно ухудшаться от одного шага к другому, т.е. вариант с неизменным значением функции не противоречит логике метода. Реализация этого шага изменяет статус клеток цикла. Заполненная клетка (2, 3) становится свободной, а клетка (2, 1) – заполненной нулевой поставкой. В результате этого изменяются потенциалы элементов таблицы поставок и матрица оценок свободных клеток.
IV шаг
Таблица поставок:
Таблица 7
2
 20
|  3
| -2 | ||||||
 1
|
30
| -1 | ||||||
| 3
|
20
| -3 | ||||||
| -3 | ||||||||
| 2
| 1
| -3 | ||||||
| -2 | ||||||||
Матрица оценок свободных клеток:
В =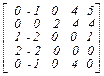 
.
Дадим поставку в клетку с отрицательной оценкой (3, 2). Цикл пересчета для этой клетки:
(1, 1) – + (1, 2)
2 0
|  | ||||||
 |  | ||||||
(2, 1) + – (2, 2)
0 3 0
Максимально возможная поставка в клетку (1, 2):
x 
= min (20, 30) = 20.
V шаг
Таблица распределения поставок:
Таблица 8
 2
| 3
| -1 | ||||||
| 1
|
 10
| -1 | ||||||
| 3
|
20
| -2 | ||||||
| -2 | ||||||||
| 2
| 1
| -2 | ||||||
| -2 | ||||||||
Матрица оценок свободных клеток:
В =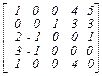 
.
Цикл пересчета для клетки (3, 2):
(1, 2) – + (1, 3)
20 20
| | ||||
| |||||
(3, 2) + – (3, 3)
20
Максимально возможная поставка в клетку (3, 2):
x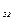 
= min (20, 20) = 20.
VI шаг
Таблица распределения поставок:
Таблица 9
|
| 3
| |||||||
| 1
|
10
| -1 | ||||||
 4
| 3
|
0
| -1 | |||||
| -1 | ||||||||
| 2
| 1
| -1 | ||||||
| -2 | -1 | |||||||
Матрица оценок свободных клеток:
В =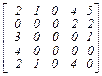 
.
Полученная матрица не содержит отрицательных элементов, что свидетельствует об оптимальности последнего базисного распределения поставок. Вычислим значение целевой функции для этого распределения:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
F = 1× 20 + 3× 10 + 3× 20 + 1× 40 + 2× 10 + 1× 60 + 1× 40 = 270.
Полученное решение является конечным решением транспортной задачи.
Варианты заданий к лабораторной работе № 4
Таблица 10
| Вариант № 1 | Вариант № 2 | ||||||||||
 M 
N 
| 
| M
N
| |||||||||
| Вариант № 3 | Вариант № 4 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 5 | Вариант № 6 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 7 | Вариант № 8 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 9 | Вариант № 10 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 11 | Вариант № 12 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 13 | Вариант № 14 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 15 | Вариант № 16 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 17 | Вариант № 18 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 19 | Вариант № 20 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 21 | Вариант № 22 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 23 | Вариант № 24 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 25 | Вариант № 26 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 27 | Вариант № 28 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 29 | Вариант № 30 | ||||||||||
| M
N
|
| M
N
| |||||||||
| Вариант № 31 | Вариант № 32 | ||||||||||
| M
N
|
| M
N
| |||||||||
|
|