
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение задачи. 1. Определим область допустимых решений задачи
|
|
1. Определим область допустимых решений задачи. Для этого последовательно рассмотрим каждое неравенство системы ограничений и дополнительные условия. В связи с тем, что каждое неравенство является нестрогим, т.е.  , уравнения, соответствующие им, являются их частными случаями. При этом каждому уравнению будет соответствовать прямая линия, построенная в координатных осях X
, уравнения, соответствующие им, являются их частными случаями. При этом каждому уравнению будет соответствовать прямая линия, построенная в координатных осях X  X
X  . Для построения прямой необходимо иметь две точки. Например, для первого уравнения: x
. Для построения прямой необходимо иметь две точки. Например, для первого уравнения: x 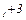 x
x  . Первая точка: x
. Первая точка: x  ; x
; x  Вторая точка:
Вторая точка: 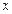
 ; x
; x  Прямая, проведенная через эти точки, делит координатную плоскость на две полуплоскости. В одной из них лежат Множество решений совместной системы m линейных неравенств с двумя переменными является выпуклым многоугольником (или выпуклой многоугольной областью). Оптимальное решение задачи линейного программирования располагается в одной из угловых точек многоугольника решений.. Если линейная функция принимает экстремальное значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек, т.е. располагается на отрезке, соединяющем точки..
Прямая, проведенная через эти точки, делит координатную плоскость на две полуплоскости. В одной из них лежат Множество решений совместной системы m линейных неравенств с двумя переменными является выпуклым многоугольником (или выпуклой многоугольной областью). Оптимальное решение задачи линейного программирования располагается в одной из угловых точек многоугольника решений.. Если линейная функция принимает экстремальное значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек, т.е. располагается на отрезке, соединяющем точки..
Многоугольник допустимых решений задачи может быть построен геометрическим методом (см. пример решения). Оптимальное решение выбирается либо путем перебора угловых точек, либо с использованием понятия линии уровня. Линией уровня линейной функции F называется линия, вдоль которой эта функция принимает одно и то же фиксированное значение F=a.
Пример
Решить задачу линейного программирования геометрическим методом.
|
|
