
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Прежде всего, обратим внимание на систему ограничений задачи
|
|
Прежде всего, обратим внимание на систему ограничений задачи. Она задана в виде нестрогих неравенств и выделяет область решений задачи. Этой областью является сектор круга радиуса в две единицы, с центром в начале координат в первом квадранте координатной плоскости X  X
X  .
.
Далее определим вид целевой функции (выпуклая или вогнутая) с использованием критерия Сильвестра. Для этого найдем вторые частные производные целевой функции:
 = 4 x
= 4 x  – x
– x  – 1;
– 1;  = – x
= – x  + 2 x
+ 2 x  – 1;
– 1;
 = 4;
= 4; 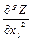 = 2;
= 2;  = – 1.
= – 1.
Матрица вторых производных имеет вид  . Первый главный минор матрицы
. Первый главный минор матрицы  = 4 > 0. Второй главный минор
= 4 > 0. Второй главный минор
 =
=  = 7 > 0.
= 7 > 0.
Оба главных минора матрицы вторых производных положительны, что свидетельствует о том, что функция выпукла в области допустимых решений задачи. В соответствии с этим определим минимум целевой функции, используя расчетную зависимость
X  = X
= X  –
–  ∙
∙  Z(Х
Z(Х  ).
).
Запишем общее выражение градиента целевой функции через первые производные
 Z = (4 x
Z = (4 x  – x
– x  – 1; – x
– 1; – x  + 2 x
+ 2 x  – 1).
– 1).
В качестве исходной возьмем произвольную точку в области решений, например, X  = (1; 1).
= (1; 1).
I шаг
X  = (1; 1),
= (1; 1),  Z
Z  = (4∙ 1 – 1– 1; – 1 + 2∙ 1 – 1) = (2; 0).
= (4∙ 1 – 1– 1; – 1 + 2∙ 1 – 1) = (2; 0).
X  = X
= X  –
–  ∙
∙  Z
Z  = (1; 1) –
= (1; 1) –  (2; 0) = (1– 2
(2; 0) = (1– 2  ; 1).
; 1).
 Z
Z  = (4(1– 2
= (4(1– 2  ) – 1– 1; –1 +2
) – 1– 1; –1 +2  +2∙ 1 – 1) = (2 – 8
+2∙ 1 – 1) = (2 – 8  ; 2
; 2  ).
).
 Z
Z  ∙
∙  Z
Z  = (2; 0)∙ (2 – 8
= (2; 0)∙ (2 – 8  ; 2
; 2  ) = 4 – 16
) = 4 – 16  + 0∙ 2
+ 0∙ 2  = 4 – 16
= 4 – 16  = 0,
= 0,  =
=  .
.
Х  =
=  ,
,  Z
Z  =
= 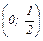 .
.
II шаг. Вместо  Z
Z  возьмем l
возьмем l  = (0; 1), вектор, по направлению совпадающий с направлением вектора градиента, но имеющий более простой вид для проведения вычислительных процедур (эту операцию не обязательно выполнять). Тогда
= (0; 1), вектор, по направлению совпадающий с направлением вектора градиента, но имеющий более простой вид для проведения вычислительных процедур (эту операцию не обязательно выполнять). Тогда
Х  = X
= X  –
–  ∙ l
∙ l  = (1/2; 1) –
= (1/2; 1) –  (0; 1) = (1/2; 1 –
(0; 1) = (1/2; 1 –  ).
).
 Z
Z  = (4∙ 1/2 – (1 –
= (4∙ 1/2 – (1 –  – 1; –1/2 + 2(1 –
– 1; –1/2 + 2(1 –  ) – 1) = (
) – 1) = ( ; 1/2 – 2
; 1/2 – 2  ).
).
l  ∙
∙  Z
Z  = (0; 1)(
= (0; 1)( ; 1/2 – 2
; 1/2 – 2  ) = 0∙
) = 0∙  +1∙ (1/2 – 2
+1∙ (1/2 – 2  ) = 1/2 – 2
) = 1/2 – 2  = 0.
= 0.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 = 1/4.
= 1/4.
X  = (1/2; 3/4);
= (1/2; 3/4);  Z
Z  = (1/4; 0).
= (1/4; 0).
III шаг. Возьмем l  = (1; 0) вместо
= (1; 0) вместо  Z
Z  .
.
X  = X
= X  –
–  ∙ l
∙ l  = (1/2; 3/4) –
= (1/2; 3/4) –  (1; 0) = (1/2 –
(1; 0) = (1/2 –  ; 3/4).
; 3/4).
 Z
Z  = (4(1/2 –
= (4(1/2 –  ) – 3/4 – 1; – 1/2 +
) – 3/4 – 1; – 1/2 +  +2∙ 3/4 – 1) = (1/4 – 4
+2∙ 3/4 – 1) = (1/4 – 4  ;
;  ).
).
l  ∙
∙  Z
Z  = 1∙ (1/4 – 4
= 1∙ (1/4 – 4  ) + 0∙
) + 0∙  = 1/4 – 4
= 1/4 – 4  = 0;
= 0;  = 1/16.
= 1/16.
X  = (7/16; 3/4);
= (7/16; 3/4);  Z
Z  = (0; 1/16).
= (0; 1/16).
IV шаг. Берем l  = (0; 1). Получим:
= (0; 1). Получим:
X  = X
= X  –
–  ∙ l
∙ l  = (7/16; 3/4) –
= (7/16; 3/4) –  ∙ (0; 1) = (7/16; 3/4 –
∙ (0; 1) = (7/16; 3/4 –  ).
).
 Z
Z  = (4∙ 7/16 – 3/4 +
= (4∙ 7/16 – 3/4 +  – 1; – 7/16 + 3/2 – 2
– 1; – 7/16 + 3/2 – 2  – 1) = (
– 1) = ( ; 1/16 – 2
; 1/16 – 2  ).
).
l  ∙
∙  Z
Z  = 0∙
= 0∙  + 1∙ (1/16 – 2
+ 1∙ (1/16 – 2  ) = 0;
) = 0;  = 1/32.
= 1/32.
X  = (7/16; 3/4 –
= (7/16; 3/4 –  ) = (7/16; 23/32) = (0, 4375; 0, 71875);
) = (7/16; 23/32) = (0, 4375; 0, 71875);
 Z
Z  = (1/32; 0) = (0, 03125; 0).
= (1/32; 0) = (0, 03125; 0).
V шаг. Берем l  = (1; 0). Тогда:
= (1; 0). Тогда:
X  = X
= X  –
–  ∙ l
∙ l  = (7/16; 23/32) –
= (7/16; 23/32) –  ∙ (1; 0) = (7/16 –
∙ (1; 0) = (7/16 –  ; 23/32).
; 23/32).
 Z
Z  = (7/4 – 4
= (7/4 – 4  – 23/32 – 1; – 7/16 +
– 23/32 – 1; – 7/16 +  + 23/16 – 1) = (1/32 – 4
+ 23/16 – 1) = (1/32 – 4  ;
;  ).
).
l  ∙
∙  Z
Z  = 1∙ (1/32 – 4
= 1∙ (1/32 – 4  ) + 0∙
) + 0∙  = 1/32 – 4
= 1/32 – 4  = 0.
= 0.  = 1/128.
= 1/128.
X  = (55/128; 23/32) = (0, 4296875; 0, 71875).
= (55/128; 23/32) = (0, 4296875; 0, 71875).
Сравнение X  и X
и X  показывает, что координаты этих точек отличаются меньше, чем на 0, 01, и поэтому последнюю точку можно считать решением задачи. Округляя, получим Х
показывает, что координаты этих точек отличаются меньше, чем на 0, 01, и поэтому последнюю точку можно считать решением задачи. Округляя, получим Х  = (0, 43; 0, 72).
= (0, 43; 0, 72).
Замечание. При выполнении отчета по лабораторной работе необходимо включить графическую часть, в которой показать область допустимых решений задачи и изобразить точки для каждого шага решения.
|
|
