
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условие задачи
|
|
Система ограничений:
x  +3x
+3x 

2x  +x
+x 
 (1)
(1)
x 

3x 
 .
.
Дополнительные условия:
x  x
x  (2)
(2)
Линейная функция:
F =2x 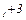 x
x  max. (3)
max. (3)
Сформулированная задача имеет вполне определенный экономический смысл. Допустим, некоторая фирма, занимающаяся выпуском металлоизделий, планирует производство двух видов продукции, например, оконных решеток и металлических дверей. Для выпуска этой продукции необходимы ресурсы четырех видов, например, металлический уголок двух видов (типоразмеров), пруток и листовой металл. Фирма располагает запасами ресурсов названных видов (правые части системы ограничений): 18 погонных метров уголка первого вида, 16 погонных метров уголка второго вида, 5 квадратных метров листового материала и 21 погонный метр прутка. Необходимо составить такой план выпуска продукции (количество решеток x  и дверей x
и дверей x  ) из имеющихся ресурсов, который обеспечил бы получение фирме максимальной выручки.
) из имеющихся ресурсов, который обеспечил бы получение фирме максимальной выручки.
Неравенства системы ограничений отражают условия баланса ресурсов. Так, первое неравенство показывает, что количество уголка первого вида, пошедшего в производство, не может превышать его запаса (т.е. 18 погонных метров). Коэффициенты при переменных x  и x
и x  имеют следующий смысл: 1 – количество погонных метров уголка первого вида, идущее на выпуск одной оконной решетки; 3 - количество погонных метров того же уголка для выпуска одной металлической двери. Сумма в левой части неравенства показывает затраты уголка на производство продукции обоих видов.
имеют следующий смысл: 1 – количество погонных метров уголка первого вида, идущее на выпуск одной оконной решетки; 3 - количество погонных метров того же уголка для выпуска одной металлической двери. Сумма в левой части неравенства показывает затраты уголка на производство продукции обоих видов.
Значение целевой функции F равно выручке предприятия от реализации произведенной продукции. Коэффициенты при переменных имеют смысл: 2 (например, 2 тысячи рублей) – выручка от реализации одной решетки; 3 – выручка от реализации одной двери.
Рассмотрим алгоритм реализации симплексного метода. Он включает следующие действия.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
1. Преобразовать неравенства системы ограничений в уравнения введением дополнительных переменных.
2. Разбить переменные задачи на две группы: основные, значения которых больше или равны нулю; неосновные, значения которых строго равны нулю. Количество основных переменных должно быть равно числу уравнений системы. Эта процедура позволяет исключить из рассмотрения неосновные переменные и получить замкнутую систему уравнений, имеющую единственное решение.
3. Выразить основные переменные через несновные и получить первоначальное базисное решение (базисным называется решение, удовлетворяющее системе ограничений и дополнительным условиям).
4. Получить выражение целевой функции через неосновные переменные. С использованием критерия оптимальности установить не является ли полученное базисное решение оптимальным. Если оно оптимально, остановить решение, если нет – продолжить. Для этого с использование выражения целевой функции через неосновные переменные установить какую из неосновных переменных перевести в основные и продолжить решение с новым набором переменных.
I шаг
Преобразуем неравенства системы ограничений в уравнения:
x  +3x
+3x  +x
+x  = 18,
= 18,
2x  + x
+ x  + x
+ x  = 16,
= 16,
x  + x
+ x  = 5,
= 5,
3x  + x
+ x  = 21.
= 21.
Система состоит из 4-х уравнений и включает 6 переменных. Разделим переменные задачи на основные и неосновные. При решении задачи на максимум целевой функции на первом шаге решения при выборе основных переменных можно воспользоваться правилом: в качестве основных переменных следует выбрать (если возможно) такие переменные, каждая из которых входит только в одно из уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входила бы ни одна из этих переменных.
Этому правилу удовлетворяют дополнительные переменные x  , x
, x  , x
, x  , x
, x  . В соответствии с этим переменные разделятся на две группы.
. В соответствии с этим переменные разделятся на две группы.
Основные переменные: x  , x
, x  , x
, x  , x
, x  .
.
Неосновные переменные: x  , x
, x  .
.
Выразим основные переменные через неосновные
x  = 18- x
= 18- x  - 3x
- 3x  ,
,
x  = 16-2x
= 16-2x  - x
- x  ,
,
x  = 5 - x
= 5 - x  , (4)
, (4)
x  = 21 - 3x
= 21 - 3x  .
.
Положив неосновные переменные равными нулю, т.е. x  = 0, x
= 0, x  = 0, получим базисное решение Х
= 0, получим базисное решение Х  = (0; 0; 18; 16; 5; 21), которое соответствует вершине О(0; 0) многогранника на рис. 1. В связи с тем, что решение является допустимым, оно может быть и оптимальным. Выразим целевую функцию через неосновные переменные. Правило выбора основных переменных на первом шаге решения обеспечивает первоначальное выражение целевой функции F =2x
= (0; 0; 18; 16; 5; 21), которое соответствует вершине О(0; 0) многогранника на рис. 1. В связи с тем, что решение является допустимым, оно может быть и оптимальным. Выразим целевую функцию через неосновные переменные. Правило выбора основных переменных на первом шаге решения обеспечивает первоначальное выражение целевой функции F =2x 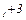 x
x  . Значение целевой функции в этом случае равно нулю.
. Значение целевой функции в этом случае равно нулю.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Однако перевод любой из неосновных переменных в основные может привести к увеличению значения функции F, т.к. коэффициенты при этих переменных положительны. Возникает вопрос, какую из двух переменных следует переводить в основные. Можно высказать предположение (но не более того), что перевод переменной x  в основные приведет к более сильному увеличению значения F в связи с большим значением коэффициента в выражении целевой функции. Этот перевод должен привести к получению нового базисного решения, в котором количество основных и неосновных переменных так же как на первом шаге должно быть равно 4 и 2, соответственно.
в основные приведет к более сильному увеличению значения F в связи с большим значением коэффициента в выражении целевой функции. Этот перевод должен привести к получению нового базисного решения, в котором количество основных и неосновных переменных так же как на первом шаге должно быть равно 4 и 2, соответственно.
В связи с этим необходимо выяснить, какая из основных переменных должна перейти в разряд неосновных. Система (4) накладывает ограничения на значение переменной x  , следующие из условия неотрицательности основных переменных. Преобразуем (4) с учетом того, что переменная x
, следующие из условия неотрицательности основных переменных. Преобразуем (4) с учетом того, что переменная x  по-прежнему остается неосновной, т.е. равной нулю.
по-прежнему остается неосновной, т.е. равной нулю.
x  = 18 - 3x
= 18 - 3x 
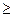 0,
0,
x  = 16 - x
= 16 - x 
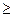 0,
0,
x  = 5 - x
= 5 - x 
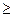 0,
0,
x  = 21.
= 21.
Отсюда следует: (x 
 6; x
6; x 
 16; x
16; x 
 5). Каждое уравнение системы (4), кроме последнего, определяет максимально возможное значение x
5). Каждое уравнение системы (4), кроме последнего, определяет максимально возможное значение x  , при котором значение соответствующей основной переменной остается неотрицательным. Последнее уравнение не накладывает ограничений на значение x
, при котором значение соответствующей основной переменной остается неотрицательным. Последнее уравнение не накладывает ограничений на значение x  , т.к. при любом значении переменной x
, т.к. при любом значении переменной x  x
x  = 21, т.е. неотрицательно. Условно этот факт фиксируется записью x
= 21, т.е. неотрицательно. Условно этот факт фиксируется записью x 

 .
.
Очевидно, что сохранение неотрицательности всех переменных возможно, если не нарушится ни одна из полученных во всех уравнениях границ. Отсюда следует, что x  = min(6; 16; 5;
= min(6; 16; 5;  ) = 5. С учетом дополнительного условия (2) интервал допустимых значений включает 0
) = 5. С учетом дополнительного условия (2) интервал допустимых значений включает 0  x
x 
 5. Однако мы заинтересованы в максимально возможном увеличении значения целевой функции, в связи с чем выбираем наибольшее значение x
5. Однако мы заинтересованы в максимально возможном увеличении значения целевой функции, в связи с чем выбираем наибольшее значение x  = 5. При этом значении переменная x
= 5. При этом значении переменная x  обращается в нуль и переходит в разряд неосновных. Третье уравнение системы (4), переводящее основную переменную в неосновные называется разрешающим и выделяется рамкой.
обращается в нуль и переходит в разряд неосновных. Третье уравнение системы (4), переводящее основную переменную в неосновные называется разрешающим и выделяется рамкой.
II шаг
Основные переменные: x  ; x
; x  ; x
; x  ; x
; x  .
.
Неосновные переменные: x  ; x
; x  .
.
Выразим основные переменные через неосновные, начиная с разрешающего уравнения
x  = 5 - x
= 5 - x  ,
,
x  = 18 - x
= 18 - x  - 3(5 - x
- 3(5 - x  ), (5)
), (5)
x  = 16 - 2 x
= 16 - 2 x  - (5 - x
- (5 - x  ),
),
x  = 21 - 3 x
= 21 - 3 x  .
.
После преобразования получим
x  = 5 - x
= 5 - x  ,
,
x  = 18 - x
= 18 - x  + 3 x
+ 3 x  ,
,
x  = 11 - 2 x
= 11 - 2 x  + x
+ x  ,
,
x  = 21 - 3 x
= 21 - 3 x  .
.
Второе базисное решение Х  = (0; 5; 3; 11; 0; 21) является допустимым и соответствует вершине А(0; 5) многоугольника на рис.1.
= (0; 5; 3; 11; 0; 21) является допустимым и соответствует вершине А(0; 5) многоугольника на рис.1.
Выразив целевую функцию через неосновные переменные, получим
F =2x 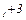 x
x  = 2 x
= 2 x  + 3 x
+ 3 x  = 2 x
= 2 x  + 3(5 - x
+ 3(5 - x  ) = 15 + 2 x
) = 15 + 2 x  - 3 x
- 3 x  .
.
Значение целевой функции F  = 15 не является максимальным, т.к. имеется возможность его увеличения переводом переменной x
= 15 не является максимальным, т.к. имеется возможность его увеличения переводом переменной x  в основные. Система уравнений (5) определяет наибольшее возможное значение x
в основные. Система уравнений (5) определяет наибольшее возможное значение x  = min(
= min( ; 3; 11/2;
; 3; 11/2;  ) = 3. Второе уравнение является разрешающим, а переменная x
) = 3. Второе уравнение является разрешающим, а переменная x  переходит в неосновные.
переходит в неосновные.
|
|
