Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

В бесконечной среде

Бесконечная среда с равномерно распределенными источниками

Радиоактивные β –нуклиды со средней энергией [МэВ] с удельной активностью q [Бк/г] равномерно распределены в однородной среде; в условиях радиоактивного равновесия (излученная в единице массы энергия равна поглощенной в единице массы энергии) мощность дозы

, Гр/с.

1) плоский источник в бесконечной среде

Плоскость с равномерно распределенными на поверхности изотропными источниками с плотностью σ [Бк/(c·см²)] расположена в бесконечной среде (рис.1). Мощность дозы в точке А равна:

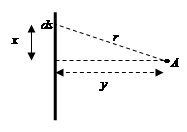
Рис.1. Геометрия расчета мощности дозы в точке А от плоского бесконечного источника

,

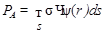где - дозовая функция β -изотопа (******). Из следующих соотношений: , , 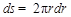следует:

.

Преобразование определяет функцию: 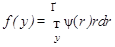, которая может быть рассчитана.

2) Толстослойный источник

Излучающий нуклид с удельной активностью q [Бк/см³] равномерно распределен в бесконечном однородном слое толщиной h, расположенном в бесконечной среде (рис.2).; определяется мощность дозы в точке А на расстоянии х от поверхности слоя. Рассматривая слой dy как тонкий источник с поверхностной активностью q·dy, определяется мощность дозы

.

В случае излучающей полубесконечной среды

. (+)

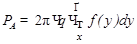Рис.2. Геометрия расчета мощности дозы в точке А от толстослойного источника

3) Полубесконечный источник в бесконечной среде

На рис. 3 показана геометрия, в которой требуется оценить мощность дозы в точке B на расстоянии х от плоскости раздела среды на два полупространства: в части I равномерно распределены источники β -излучения; часть среды II не содержит источников. Уравнение (+) определяет мощность дозы в точке А на том же расстоянии х от поверхности раздела, и эта величина равна мощности дозы в точке B при переносе источников в полупространство II.; Тогда, если мощность дозы в бесконечной среде с распределенными в ней источниками есть , то вычитая вклад полупространства II,

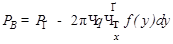
Рис.3. Полубесконечный источник в бесконечной среде

Принцип обратимости дозы

Рис.

а) Простейший пример обратимости системы «источник-детектор» в бесконечной однородной среде; источник S и детектор D изотропны. Взаимная замена местами источника и детектора не изменяет показа 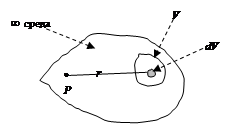ния детектора.

Рис

б) Объёмный распределенный в V изотропный источник излучений, создаваемая которым доза в точке Р равна:

;

где q (r) – удельная активность источника, 1/см³,

ψ (r) – дозовая функция точечного изотропного источника для любого вида излучения.

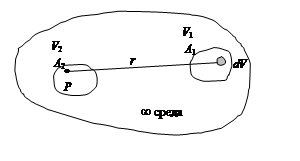А ₁ – полная активность радиоактивного нуклида в объёме V ₁,

А ₂ – полная активность радиоактивного нуклида в объёме V ₂.

Доза в точке Р, создаваемая источниками в объёме V ₁^

.

Средняя доза в объёме V ₂: ;

. (*)

Аналогично средняя доза в объёме V ₁:

(**)

Из (*) и (**) следует:

и при

,

т. е., при одинаковых полных активностях нуклидов в объёмах V ₁ и V ₂ средние дозы в объёмах независимо от их формы и размеров равны. В частности, если вся активность А ₁ сосредоточена в точке Р, то средняя доза в объёме V ₂ будет равна дозе в точке Р при переносе активности А ₁ в объём V ₂.

Следует отметить еще одно следствие из представленных выше соотношений: эквивалентность геометрий «широкий пучок – точечный детектор» и «тонкий пучок – широкий детектор» (рис.1), которая позволяет в ряде случаев оптимизировать расчетные и экспериментальные методы получения необходимой информации о характеристиках

Рис.1. Эквивалентность геометрий «широкий пучок – точечный детектор» и «тонкий пучок – широкий детектор»

Если удельные концентрации нулидов в объёмах V ₁ и V ₂ равны:, , то из (*) и (**) следует:

,

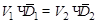что означает равенство интегральных поглощенных энергий в объёмах V ₁ и V ₂.