Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Камерные модели.

Дифференциальное уравнение для i – ой камеры:

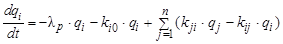, где

- скорость уменьшения активности за счет распада нуклида;

- скорость уменьшения активности за счет процесса фиксации или выведения;

- вклад других систем в i- ю систему;

- передача активности другим системам;

, - константы переноса из одной систему в другую.

Таким образом, имеется система из n обыкновенных дифференциальных уравнений первого порядка. Задача нахождения концентраций нуклида может быть представлена в матричном виде:

, где

М – вектор-столбец концентраций активностей;

- транспортная матрица.

Простая кинематика нуклидов в рамках однокамерной модели.

Рассматривается одна система организма человека, например, циркулирующая кровь; РВ выводятся из этой системы или фиксируются в других органах и тканях. Соответствующая система обыкновенных дифференциальных уравнений, описывающая кинематику процессов перехода нуклида (схема миграции нуклида показана на рис. Н):

(2.4)

, Бк - начальная активность при t =0.

Входящие в уравнения переменные и константы:

- начальная активность нуклидав момент времени t = 0, входящего в систему, Бк;

- текущее значение активности, Бк;

- масса системы или органа, кг;

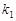- коэффициент, определяющий скорость выведения нуклида из системы, с^-1;

- постоянная распада нуклида, с^-1;

- коэффициенты, определяющие вывод нуклида в депо фиксации и резервуар выведения; .

Рис. Н. Блок – схема однокамерной модели.

Параметр , Бк/г – средняя концентрация активности в рассматриваемой системе.

Решение системы (2.4):

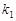+ ))∙ t;

∙ t)∙ [1-exp(-k₁· t)]; (2.5)

Первые два уравнения (2.5) определяют концентрации активностей в системе и в депо фиксации; третье уравнение - активность выводимого нуклида.

Пример:

; ; ; ; .

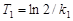Предельная концентрация активности в фиксирующей ткани:

; при t > 5 T ₁ осуществляется выход на экспоненциальную часть решения.