Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Количественная трековая авторадиография β–активных “горячих“ частиц

Термин “горячая“ частица относится к микроскопическим частицам, содержащим радиоактивные нуклиды с высокой активностью и с размерами 1 ÷ 100 мкм. Появление их связано с ядерными испытаниями, деятельностью ядерных производств и авариями на ядерно-технических установках (ядерные реакторы). Эти частицы, (в основном заряженные частицы; далее рассматриваются β – излучающие нуклиды) при попадании внутрь организма обусловливают высокий риск радиационных воздействий на ткани и органы человека. Риск оценивается на основании различных биологических моделей, при использовании которых требуется информация о функциях радиального распределения поглощенных доз в окрестности “горячей“ частицы в биологической ткани.

Существуют различные возможности установления этих распределений:

● априори предполагается, что частица содержит определенный β – изотоп с известной активностью; далее на основании функции Левинджера (разд. %%) рассчитывается зависимость «радиус–доза» в биологической ткани; естественно, что обычно исходная информация или отсутствует, или известна с большой неконтролируемой погрешностью;

● измеряется активность и энергетическое распределение (спектр) β – частиц реальной “горячей“ частицы методами

β – спектроскопии; далее на основании этой информации с использованием функции Левинджера определяется зависимость «радиус–доза»;

● реализуется подход на основании метода авторадиографии с использованием высокочувствительных толстослойных ядерных фотоэмульсий*. Измеряется и обрабатывается денситограмма плотности dG/dr проявленных зерен в объёме фотоэмульсии в радиальном направлении в окрестности “горячей“ частицы; далее это распределение преобразуется в распределение поглощенной энергии dE / dr=f (r) в эмульсии, которое трансформируется в распределение «радиус–доза» биологической ткани.

Трек β – частицы в эмульсии характеризуется полным количеством образованных зерен G, полным пробегом L и радиусом R (рис.88).

Рис.66. Параметры трека β – частицы

Зависимость числа зерен G на треке от энергии электрона Т аппроксимируется соотношением:

,

где n ₀ = 17, Т₀ = 28, 6 кэВ, w₀ = 1, б7 кэВ/зерно. Аналогичная упрощенная функция с учетом констант:

.

Зависимость “пробег–энергия” для электронов в эмульсии можно определить соотношением:

;

соответствующая связь числа зерен G с пробегом R:

.

Из данных соотношений можно получить функции радиального распределения зерен G иэнергии Е:

(++)

(R ₀– максимальный пробег электрона).

При известном β – спектре эмиссии по нему можно проинтегрировать соотношения (++):

(11)

, (22)

Т₀ – максимальная (граничная) энергия β –спектра, R (T) – радиус трека электрона с энергией Т.

Результаты расчетов по (11) и (22) для широкого набора β –спектров позволяют сделать вывод о примерно постоянном (в пределах 5¸ 10%) значении энергии w на образование зерна, т.е.

, w» 2, 35 кэВ/зерно.

Функция Левинджера был использована для расчета радиальных дозовых распределений в фотоэмульсии; было установлено, что с погрешностью ±15% оно совпадает с распределением в биологической ткани, если соответствующие толщины выражены в массовых единицах. Обработка изображения экспонированной β – частицами эмульсии проводится в соответствии с геометрией, показанной на рис. (88):

Рис. тт. К обработке экспонированной фотоэмульсии

Размер “горячей“ частицы значительно меньше R(T0) и она рассматривается как точечный изотропный источник; толщина фотоэмульсии H > R(T0). Измеряется распределение оптической плотности почернения: , , .

Объёмная плотность зерен определяется соотношениями:

, .

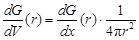Следующие соотношения устанавливают связь рассматриваемых величин:

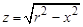; , , , . Далее устанавливается следующая связь величин:

.

Интегрирование по радиусу (плотность почернения в вертикальном направлении) определяет функцию по переменной х:

;

Это уравнение относительно неизвестной функции есть интегральное уравнение Абеля, решение которого следующее:

.

а)

Рис.11. Измеренное распределение оптической плотности почернения (а) и восстановленное дозное рспределение (б)