Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Бесконечной тканеэквивалентной среде

1. Изотропный источник β - частиц

Если β – излучающий нуклид произвольным образом распределен в однородной среде и функция) описывает распределение объёмной плотности активности ( - координаты точек источников), то величина поглощенной энергии в точке определяется интегралом:

, где

) – дозовая функция точечного изотропного источника β – частиц в данной среде. Различные аппроксимации этой функции соответствовали следующей функциональной зависимости:

,

где параметр зависит от граничной энергии бета–спектра. В настоящее время наиболее используемой оценкой пространственного дозового распределения β – частиц в тканеэквивалентной (вода) среде является соотношение Лёвинджера (Loevinger), полученное на основании аппроксимации соответствующих экспериментальных данных:

, где

к – константа размерности;

0 при 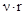= 0; параметр с в соотношении () зависит от граничной энергии Е _max β – излучателя:

с = 2, 0 при 0, 17 < E_max < 0, 5 МэВ;

с = 1, 5 при 0, 50 < E_max < 1, 0 МэВ;

с = 1, 0 при 1, 00 < E_max < 3, 0 МэВ.

Коэффициент поглощения ν определяется в основном граничной энергией бета – спектра и параметром :

, где, - средняя энергия β – спектра и - средняя энергии т.н. гипотетически разрешенного β –спектра, имеющего ту же граничную энергию (табличное значение из результатов теории β – распада).

Формула Лёвинджера обобщает экспериментальные данные для 12 β – изотопов в диапазоне граничных энергий Е _max = 0, 167 ÷ 2, 27 МэВ (³⁵S, ⁹⁰Y). Полученному соотношению присущи недостатки, проистекающее из чисто эмпирической подгонки результатов ограниченного числа измерений. Многие излучатели, ³Н, ⁶³Ni (малые граничные энергии), ¹⁰⁶Ru, ¹⁰⁶Rh, ⁴²K (большие граничные энергии) находятся вне диапазона применимости соотношения Лёвинджера. Кроме того, радиальные распределения поглощенной энергии β – частиц зависят не только от величин граничных энергий спектров, но и, в частности, от средней энергии спектров (т.е. от формы β – спектра).

Рис. Глубинное дозное распределение β – частиц изотропного источника изотопа в воде.

2. Изотропный источник γ - квантов

Вклад нерассеянной компоненты фотонов изотропного источника в дозу

)

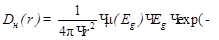
С учетом вклада всех фотонов (рассеянные и нерассеянные фотоны) величина дозы определяется соотношением:

, где

вклад многократного рассеяния фотонов учитывается введением фактора накопления B_d:

B_d = (G _нр+ G _р)/ G _нр = 1+ G _р/ G _нр > 1

где G _нр – вклад в функционал нерассеянного излучения;

G _р – вклад в функционал рассеянного излучения.

В общем виде дозовый фактор накопления для фотонов с энергией Е ₀ на расстоянии r от источника определяется соотношением:

_,

где - коэффициент поглощения энергии фотонов в среде; и - поток нерассеянного и суммарный поток рассеянного и нерассеянного излучения.

Экспоненциальное аналитическое представление фактора накопления в зависимости от расстояния r:

,

где 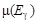– полный коэффициент поглощения фотонов;

параметры , , 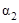- табулированные значения для данной среды и энергии фотонов.

В объёмных источниках происходят процессы поглощения и рассеяния фотонов веществом самого источника. При использовании аналитического двухэкспоненциального представления фактора накопления (1.3) функционал интенсивности фотонов I в точке объёмного источника V с удельной мощностью q_{m ,} МэВ/(с∙ кг) равен:

,

где и 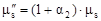; 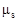- полный коэффициент ослабления фотонов.

В условиях электронного равновесия

****************************?
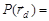