Источников β – излучения

Выход β – частиц с поверхности толстослойного источника есть величина, определяющая число частиц, выходящих с единицы площади поверхности источника в единицу времени, пропорциональная удельной активности источника. Практически необходимо количественно связать скорость счета N детектора (счетчика) с величиной удельной активности q препарата (объекта):

,

что следует из соотношения: 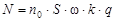, где

n₀ – выход β – частиц с единицы поверхности источника с единичной удельной активностью,

S – площадь поверхности источника,

К – поправка на поглощение частиц на пути от поверхности источника до детектора,

ω – доля вышедших из источника частиц, попадающих в счетчик.

Обычно известна величина площади поверхности источника S и параметр к определяется экспериментально; кроме того, необходима информация об угловом распределении выходящих из источника частиц для определения параметра ω, и основная величина n₀, зависящая от энергетического спектра β – частиц и атомного номера вещества источника. Соответствующая связь между значением удельной активности источника и выходом β – частиц с его поверхности может быть получено (в предположении независимости коэффициента обратного отражения β – частиц от их энергии) следующим образом: рассматривается бесконечная однородная среда (максимальный пробег электронов значительно меньше линейных размеров среды), каждый элемент объёма которой испускает электроны с энергией Е. На рис. Н показаны три геометрии, в рамках которых последовательно проводится вывод соответствующего соотношения. Определим средний путь l частиц, пересекающих слой dx. В геометрии 1 угловое распределение частиц является изотропным и ток частиц через любую плоскость в среде ~ cosθ (dl = dx/ cosθ).

Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer

Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM. SeoHammer делает продвижение сайта прозрачным и простым занятием. Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.

Что умеет делать SeoHammer

— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.

SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней.

Зарегистрироваться и Начать продвижение

Рис.Н. Геометрии расчета.

Число частиц dn^', пересекающих площадку ds, в единицу времени в единичном телесном угле 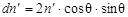, где n^' - полное число частиц, пересекающих ds. Среднее расстояние l частиц, проходящих через слой dx:

.

Если Е ₁ энергия электронов, испущенная в элементе объёма dv = dsdx, и Е ₂ – поглощенная энергия в том же объёме, то

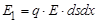и , где

– средние ионизационные потери энергии электронов

в веществе, где равномерно распределен моноэнергетический источник электронов. В условиях бесконечной геометрии Е ₁ = Е ₂^, , откуда следует:

. (ф2)

В приближении , где R – средний пробег электронов с энергией Е, соотношение (ф2) преобразуется к виду:

. (ф3)

С учетом геометрии 2, где в верхнем полупространстве среды источники отсутствуют (в итоге источников вдвое меньше), соотношение (ф3) принимает вид:

. (ф4)

(последнее соотношение определяет связь между величиной удельной активности и выходом α – частиц.

Сервис онлайн-записи на собственном Telegram-боте

Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.

Для новых пользователей первый месяц бесплатно.

Зарегистрироваться в сервисе

В геометрии 2 эффект обратного отражения электронов (альбедо) от верхнего полупространства (вклад от верхнего полупространства был просто исключен). Если коэффициент обратного отражения электронов р (р < 1), то с учетом возможности многократного пересечения электронами плоскости раздела в геометрии 2

, где n соответствует выходу частиц в геометрии 3; в последнем случае геометрия 3 определяет реальные условия измерения выхода электронов из источника:

. (ф5)

Если источники в среде являются β – излучающими нуклидами с непрерывным энергетическим распределением n (E), то в соотношении (ф5) величина пробега R заменяется усредненной по спектру n (E) зависимости R (E) (имеет место однозначная связь пробега электрона с его энергией):

, где (ф)

- граничная энергия β – спектра. Используется также приближение средняя энергия β – спектра.

Соот ношение для оценки удельной активности β – нуклидов

на основании функции ослабления частиц β – спектра.

Пусть q – удельная активность β – нуклида в среде с плотностью ρ. Из 1 см³ изотропно излучается q ρ частиц в сек. На глубине х от поверхности источника выделим объём dV = s· dx, s – площадь источника. В относительный телесный угол ω испускается

частиц и при 100% эффективности регистрации скорость счета от выделенного элемента объёма

, где

μ – коэффициент ослабления β – частиц. Полное число частиц, регистрируемое детектором

.