Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача 72

На рисунке изображены сечения трех прямолинейных бесконечно длинных проводников с токами. Расстояния АВ=ВС =5 см, токи I₁ = I₂=I и I₃ = 2 I. Найти точку на прямой АС, в которой напряженность магнитного поля, вызванного токами I₁, I₂ и I₃, равна нулю.

Дано: АВ=ВС =5 см I1 = I2=I I3 = 2 I Hрез = 0	Решение: Напряженность магнитного поля, создаваемая бесконечно длинным прямолинейным проводником:
х-?	где а - расстояние до данной точки.

1) Попробуем найти точку, в которой H_рез = 0 в отрезке АВ прямой АВС, свяжем систему координат с точкой местонахождения тока I₁, т.е. предположим местонахождение этой точки определяет точка с координатами (х, 0).

Согласно принципу суперпозиции

Спроецируем вектора на ось Оу, получаем с учетом того, что Н =0:

Н₂ - Н₁ - Н₃ = 0

Подставим в данное выражение числовые значения H₁, Н₂, Н₃, сокращая при этом на , т.к. это отношение не равно нулю. Получаем:

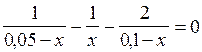
0, 15 х = 0, 005,

т.к. (0, 1- х)(0, 05- х) х ¹ 0

Отсюда

х = 0, 033 (м)

Искомая точка удалена от проводника I₁ на расстояние х =0, 033 м.

2) Предположим, что искомая точка находится на отрезке (¥, А], свяжем систему координат с точкой местонахождения проводника I₁, координата точки будет (х, О).

Согласно принципу суперпозиции

Спроецируем вектора на ось Оу, получаем с учетом того, что Н =0:

Н₂ - Н₁ + Н₃ = 0

Подставим в данное выражение числовые значения H₁, Н₂, Н₃, сокращая при этом на , т.к. это отношение не равно нулю. Получаем:

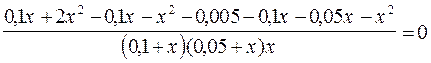
-0, 15 х = 0, 005,

т.к. (0, 1+ х)(0, 05+ х) х ¹ 0

Отсюда

х = -0, 033 (м)

Этот результат подтверждает ранее полученный. Рассматривая две ранее полученные системы координат мы видим, что полученные координаты для точки в этой системе координат совпадает с полученными координатами искомой точки в первом случае, если совмещать две системы.

3) Предположим, что искомая точка находится на отрезке ВС.

В данном случае векторная сумма не может равняться нулю, т.е. , т.к. векторы , и сонаправлены.

4) Предположим, что искомая точка находится на отрезке [С, ¥), свяжем систему координат с местонахождением проводника I₃ и координата точки будет (х, 0).

Согласно принципу суперпозиции

Спроецируем вектора на ось Оу, получаем с учетом того, что Н =0:

Н₃ - Н₁ - Н₂ = 0

Подставим в данное выражение числовые значения H₁, Н₂, Н₃, сокращая при этом на , т.к. это отношение не равно нулю. Получаем:

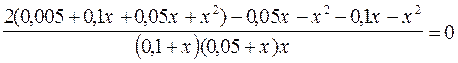
0, 15 х = - 0, 01,

т.к. (0, 1+ х)(0, 05+ х) х ¹ 0

Отсюда

х = -0, 066 (м)

Этот результат подтверждает ранее полученные, т.к. координата полученной точки совпадает с искомой, полученной в первом пункте.

Ответ: точка, в которой напряженность магнитного поля, вызванного токами I₁, I₂ и I₃ равна нулю, находится между точками I₁ и I₂ на расстоянии а =0, 033 м от точки А.