
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Заполнение электронами и дырками зон невырожденного полупроводника
|
|
Вероятность заполнения энергетического уровня для частицы с полуцелым спином (фермионов), то есть вероятность нахождения электрона на уровне с энергией E, определяется статистикой Ферми-Дирака (1.18)
 , ,
| (2.4) |
где k – постоянная Больцмана, F – энергия Ферми.
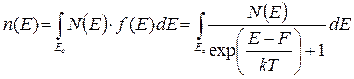 , ,
| (1.19) |
 б б
|
| Рис. 1.7 |
Для невырожденного полупроводника E-F»kT,  »1, тогда можно применить статистику Максвелла-Больцмана:
»1, тогда можно применить статистику Максвелла-Больцмана:
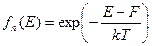 , ,
| (2.4) |
Для того чтобы рассчитать концентрацию всех свободных электронов, т.е. концентрацию электронов в зоне проводимости, необходимо проинтегрировать по всей зоне проводимости, согласно (1.19). Поскольку функция Больцмана – очень быстро спадающая экспонента, при интегрировании по зоне в качестве верхнего предела использована ∞:
 , ,
| (2.6) |
где Nс – эффективная плотность состояний в зоне проводимости или плотность квантовых состояний у дна зоны проводимости в свою зависит от температуры.
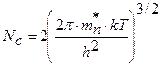 , ,
| (2.8) |
Если подставить численные значения универсальных констант, то получим:
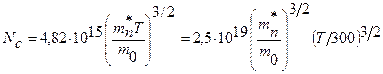 , ,
| (2.10) |
В частности для кремния:
 , ,
|
Функция распределения Ферми-Дирака для дырок имеет вид:
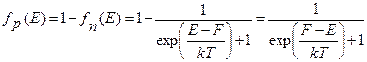 , ,
| (2.5) |
Функция распределения Максвелла-Больцмана для дырок
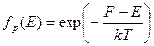 . .
| (2.5) |
Для расчета общего количества свободных дырок выполним интегрирование по валентной зоне:
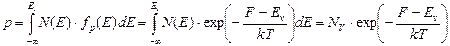
| (2.7) |
Эффективные плотности состояний для валентной зоны:
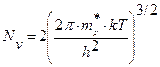
| (2.9) |
Для кремния
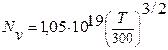
|
Значения эффективной плотности состояний для основных полупроводниковых материалов при комнатной температуре представлены в следующей таблице.
| Свойство | Ge | Si | GaAs |
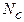 , см-3 , см-3
| 1, 02ּ 1019 | 2, 8ּ 1019 | 4, 7ּ 1017 |
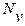 , см-3 , см-3
| 6, 1ּ 1018 | 1, 0ּ 1019 | 7, 0ּ 1018 |
Графически концентрации электронов и дырок можно определить согласно рис. 2.7.
|
|
