
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Зонная теория твердого тела
|
|
При объединении атомов в кристалл значение энергии атома изменяется по отношению к изолированному атому: появляется диэлектрическая проницаемость  , ядра кристаллической решетки создают потенциальное поле
, ядра кристаллической решетки создают потенциальное поле  . Рассмотрим кристаллическую решетку с периодом аn.
. Рассмотрим кристаллическую решетку с периодом аn.
Электрон, находящийся на орбитали атома, связан со «своим» ядром, вероятность его перемещения по кристаллу под воздействием температуры или внешнего электрического поля мала. Говорят, что такой «квазисвязанный» электрон находится в «потенциальной яме». Под влиянием внешних факторов (света, температуры и т.д.) электрон может увеличить свою кинетическую энергию и перейти на следующий энергетический уровень, вплоть до полного освобождения от влияния «своего» ядра.
а 
|  б
б
|
 в
в
| |
| Рис. 1.1 |
При сближении атомов потенциальные кривые частично налагаются друг на друга (штриховая линия рис. 1.1, б) и дают результирующий потенциальный рельеф (сплошные линии) с пониженными потенциальными барьерами между атомами. Говорят, что валентные электроны обобществляются, и каждый электрон теперь принадлежит всему кристаллу.
До тех пор, пока электрон будет находиться в кристалле, он будет не совсем свободен, то есть находиться в периодическом поле всей решетки кристалла. Другими словами даже «свободный» электрон будет принадлежать всем образующим кристалл атомам. При этом электрон получает возможность беспрепятственно перемещаться по кристаллу от атома к атому без изменения энергии.
Как видно из рис. 1.1, потенциальная энергия  =
=  , где
, где  (x, y, z) - радиус-вектор данной точки пространства,
(x, y, z) - радиус-вектор данной точки пространства,  - вектор кристаллической решетки. При повышении энергии электрона возрастает вероятность его туннелирования через потенциальный барьер (для туннелирования в квантовой механике не обязательно, чтобы энергия электрона стала больше максимума потенциальной ямы). С другой стороны, даже «свободный» электрон под влиянием потенциального поля может изменить свою траекторию, то есть потерять (рассеять) часть своей кинетической энергии в направлении
- вектор кристаллической решетки. При повышении энергии электрона возрастает вероятность его туннелирования через потенциальный барьер (для туннелирования в квантовой механике не обязательно, чтобы энергия электрона стала больше максимума потенциальной ямы). С другой стороны, даже «свободный» электрон под влиянием потенциального поля может изменить свою траекторию, то есть потерять (рассеять) часть своей кинетической энергии в направлении  . Говорят, что такой «квазисвободный» электрон движется в периодическом поле кристаллической решетки.
. Говорят, что такой «квазисвободный» электрон движется в периодическом поле кристаллической решетки.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Каждый энергетический уровень изолированного атома в кристалле расщепляется в зону.

|
| Рис. 1.2. Зонная диаграмма |
Энергетические зоны в общем случае разделены запрещенными для электронов энергетическимизазорами (щелями), называемыми запрещенными зонами Eg (g – от gap – промежуток, щель). С ростом энергии (главного квантового числа) ширина энергетических зон увеличивается, а ширина запрещенных зон уменьшается.
Оценим среднее расстояние между соседними уровнями энергии в разрешенной зоне. Пусть постоянная решетки а =0, 4 нм, то есть а3=64·10-24 см3. Количество элементарных ячеек в объеме V=1 см3 равно числу состояний в зоне:  . При ширине зоны 1 эВ среднее расстояние между ее уровнями ~ 10-22 эВ, то есть энергетическую зону можно считать квазинепрерывной.
. При ширине зоны 1 эВ среднее расстояние между ее уровнями ~ 10-22 эВ, то есть энергетическую зону можно считать квазинепрерывной.
На любом энергетическом уровне в разрешенной зоне в соответствии с принципом Паули могут находиться не более двух электронов с противоположно направленными спинами.
Число квантовых состояний в зоне равно общему числу мест на уровнях изолированных атомов, из которых образовалась эта зона, таким образом, на N уровнях могут находиться не более 2N электронов.
Рассмотрим последнюю полностью или частично заполненную зону, сформированную из валентных электронов и следующую за ней, то есть зону энергий, соответствующую энергиям электронов, разорвавших связь с атомами, но не покинувших кристалл.
В каждой энергетической зоне энергия электрона является функцией его квазиимпульса (волнового вектора):  =
=  . На рис.1.3 для двух смежных зон представлены простейшие зависимости E (k), характерные для кубического кристалла. Вблизи экстремумов мы получаем параболическое изменение энергии.
. На рис.1.3 для двух смежных зон представлены простейшие зависимости E (k), характерные для кубического кристалла. Вблизи экстремумов мы получаем параболическое изменение энергии.

|
|
| Рис. 1.3. Энергетическая диаграмма | Упрощенная энергетическая диаграмма |
Верхняя зона называется зоной проводимости, поскольку зона имеет множество свободных состояний, попавшие в неё электроны могут перемещаться под действием внешних полей, изменяя свое положение и энергию, т.е. создавая токи проводимости.
Нижняя зона – валентная. Электрон попасть в зону проводимости из валентной зоны может, только преодолев запрещенную зону величиной Eg. Энергетический уровень, соответствующий дну зоны проводимости принято обозначать Ec. Энергетический уровень, соответствующий потолку валентной зоны обозначают Ev.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Таким образом, Eg = Eс – Ev.
В зависимости от положения экстремумов энергетических зон различают прямозонные и непрямозонные полупроводники (рис. 1.4).

|
| Рис. 1.4. Зонная диаграмма |
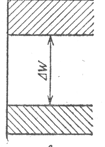
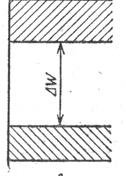
Ширина запрещенной зоны Eg - одна из важнейших характеристик вещества и может принимать как положительные (для диэлектриков и полупроводников), так и отрицательные значения. В последнем случае дно зоны проводимости будет находиться при энергиях меньших, чем потолок валентной зоны. На рис.1.5 приведена схема энергетических зон для полупроводников, диэлектриков и металлов.

| 
|  
|
| Рис. 1.5. |
Полупроводники и диэлектрики отличаются только шириной запрещенной зоны. Так, у диэлектриков ширина запрещенной зоны, как правило, больше 4 эВ. При комнатной температуре тепловой энергии недостаточно для заброса электронов из валентной зоны в зону проводимости. Для металлов характерно отсутствие запрещенной зоны.
При воздействии на кристалл температуры и давления изменяются расстояния между атомами, области перекрытия волновых функций. Это вызывает изменение ширины энергетических и запрещенных зон.
 , ,
| (1.17) |
| Рис. 1.6. Температурная зависимость Eg для кремния |
Значения  близки к единице,
близки к единице,  - температурный коэффициент изменения ширины запрещенной зоны.
- температурный коэффициент изменения ширины запрещенной зоны.  < 0 для большинства полупроводников.
< 0 для большинства полупроводников.
Значения  ,
,  и
и  для основных полупроводников, применяемых в микроэлектронике приведены в табл. 1.1.
для основных полупроводников, применяемых в микроэлектронике приведены в табл. 1.1.
Таблица 1.1.
Значение Eg и  для некоторых полупроводников
для некоторых полупроводников
| Полупроводники | Ge | Si | GaAs |
| Eg(T =300K), эВ | 0, 66 | 1, 11 | 1, 43 |
 (T=0K), эВ (T=0K), эВ
| 0, 74 | 1, 166 | 1, 52 |
 , эВ·К-1 , эВ·К-1
| -2, 4·10-4 | -3, 9·10-4 | -4, 3·10-4 |
Для свободного электрона мы записывали  =
=  .Отличие свободного электрона, от электрона, находящегося в кристалле в его эффективной массе, определяемой как:
.Отличие свободного электрона, от электрона, находящегося в кристалле в его эффективной массе, определяемой как:
 . .
| (1.21) |
Вторая производная характеризует степень крутизны зависимости E(k), чем круче эта зависимость, тем меньше масса электрона. Эффективная масса электрона в кристалле зависит от его энергии и является характеристикой материала.
| Вставить рис. с разными m |
| Рис. 1.7 |
До сих пор мы рассматривали случай, когда уровень Ферми находится в разрешенной зоне. Такой полупроводник называется вырожденным. В невырожденном полупроводнике уровень Ферми находится между зоной проводимости и валентной зоной, то есть внутри запрещенной зоны.
Глава 2. Электропроводность полупроводников
Электропроводность полупроводников зависит от количества электронов в зоне. Если валентная зона заполнена не полностью, то часть из находящихся в ней электронов также приобретает способность участвовать в электропроводности. Для характеристики переноса заряда электронами валентной зоны введена виртуальная частица – дырка *, обладающая положительным зарядом. Таким образом, перенос заряда в твердом теле может осуществляться как электронами, находящимися в зоне проводимости так и дырками, находящимися в валентной зоне.
Вводя в кристалл примеси, можно увеличивать концентрацию свободных электронов или дырок и таким образом увеличивать проводимость кристалла, делая её преимущественно дырочной или электронной.
|
|
