Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Собственные и легированные полупроводники. Уравнение электронейтральности

Если валентному (связанному) электрону сообщить энергию равную E_g, образуется пара электрон-дырка, то есть образуются две частицы, которые могут принять участие в электропроводности, имеющие противоположные заряды. На образование одной частицы требуется энергия активации, равная Е_а=E_g/2. Энергия, необходимая для увеличения концентрации носителей на единицу, называется энергией Ферми. Для чистого (беспримесного, собственного) полупроводника уровень Ферми находится примерно в середине запрещенной зоны (примерно, так как ) (см. подраздел 2.2.1). В собственном полупроводнике всегда выполняется равенство n₀=p₀=n_i [см^-3]. Концентрации носителей, находящихся в термодинамическом равновесии, равны между собой и равны собственной концентрации.

Рис. 2.1 Кристалл собственного полупроводника

Вблизи дна зоны проводимости зависимость энергии электрона от величины импульса (или волнового числа k):

(2.1)

В пространстве k (p) мы имеем параболическую зависимость энергии (рис.2.3, а). Обычно энергия свободного электрона (электрона в зоне проводимости) отсчитывается от E_с - энергии дна зоны проводимости, иногда от уровня Ферми. Ось, характеризующая кинетическую энергию дырок, направлена в противоположную сторону:

(2.2)

где E_v – энергия потолка валентной зоны, - эффективная масса дырок, определяемая аналогично (1.21).

Рис. 2.2. Упрощенная энергетическая диаграмма собственного полупроводника

Энергия дырки отсчитывается от E_v, иногда от уровня Ферми, чем большей энергией обладает дырка, тем ниже от E_v она опускается. Дырки с минимальной энергией будут скапливаться у потолка валентной зоны, электроны - у дна зоны проводимости. Отметим, что положение E_с и E_v не всегда совпадают в () пространстве При совпадении их полупроводник называют прямозонным, в противном случае полупроводник называется непрямозонным. GaAs является прямозонным полупроводником, Si и Ge – непрямозонными (рис. 2.3).

Рис. 2.3, а. Энергетическая диаграмма прямозонного полупроводника	Рис. 2.3б. Энергетическая диаграмма непрямозонного полупроводника

В дальнейшем мы будем использовать упрощенную энергетическую диаграмму (рис. 2.2).

Образовавшиеся в результате разрыва ковалентной связи (генерации) электрон и дырка хаотично передвигаются по кристаллу до тех пор, пока электрон не будет захвачен дыркой, то есть не произойдет рекомбинация. Промежуток времени, прошедший с момента генерации частиц до их рекомбинации, называется временем жизни носителей.

Наличие в кристалле примесей приводит к появлению в запрещенной зоне энергетических уровней, положение которых зависит от типа примеси (рис. 2.4).

Рис. 2.4

Для управления электрическими свойствами полупроводников в них специально вводят примеси (легируют). Необходимо подчеркнуть, что при замещении атома кристалл остается электронейтральным! Только при ионизации атомов примеси, например, при введении в полупроводник IV группы периодической системы элементов (например, Si) примеси элементов V группы – доноров появляются дополнительные электроны, введение элементов III группы – акцепторов – приводит к появлению дополнительных дырок.

На рис.2.5 показана схема решетки кристалла Si, в который введен фосфор (V группа). Элемент V группы имеет 5 валентных электронов, четыре из них образуют связи с соседними атомами Si, пятый электрон связан только с атомом примеси, и эта связь слабее остальных, поэтому при нагреве кристалла пятый электрон отрывается первым, при этом атом фосфора приобретает положительный заряд, становясь ионом .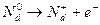

Рис. 2.5

Энергия ионизации доноров (E_d), как правило, невелика и при комнатной температуре донорная примесь отдает свои электроны, поэтому такие полупроводники и называют электронными или полупроводниками n-типа, а электроны – основными носителями заряда. Дырки в электронном полупроводнике являются неосновными носителями.

Введение донорной примеси приводит к увеличению концентрации электронов (при её ионизации) и, соответственно, к смещению уровня Ферми к зоне проводимости (чем он ближе к ней, тем больше концентрация электронов).

Рассмотрим, что происходит при введении в тот же кремний элемента III группы, например, бора. Элемент III группы имеет 3 валентных электрона, которые образуют связи с соседними атомами Si, дополнительная четвертая связь с Si может образовываться, если к атому бора от одного из его ближайших соседей перейдет еще один электрон (cм. рис. 2.6). Энергия такого перехода невелика, поэтому энергетический уровень акцептора, принимающего электрон, расположен вблизи валентной зоны. При этом атом бора ионизуется, заряжаясь отрицательно, а в том месте, откуда ушел электрон, образуется положительно заряженная дырка, которая может участвовать в переносе заряда: .

Рис. 2.6

Энергия ионизации акцепторов E_a< < E_g, и при комнатной температуре акцепторная примесь ионизованна, поэтому такие полупроводники и называют полупроводниками p-типа, а дырки – основными носителями заряда. Электроны в полупроводнике p-типа являются неосновными носителями. Введение акцепторной примеси приводит к смещению уровня Ферми к валентной зоне.

Для собственного полупроводника можно записать уравнение электронейтральности:

,

(2.3)

Если в полупроводнике присутствуют как донорная, так и акцепторная примесь, можно записать уравнение электронейтральности:

,

(2.3, а)

где q – заряд электрона, n – концентрация электронов в зоне проводимости, образовавшиеся за счет обрыва связи с «собственным» полупроводником (в нашем случае с кремнием) и с донорной примесью, p – концентрация дырок в валентной зоне, образовавшиеся за счет обрыва связи с «собственным» полупроводником и за счет акцепторной примеси, - концентрация ионизированных (захвативших электрон) ионов акцепторной примеси, - концентрация ионизированных (отдавших электрон) ионов донорной примеси.