
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Совместное решение (8.17) и (8.17а) дает
|
|
 |
Если корни характеристического уравнения являются комплексно-сопряженными, то в (8.16) сопряжены не только p1 и p2 (p1, 2 = — d ± jw), но и A1 и A2. Поэтому свободный ток
Угловая частота w0 и коэффициент затухания d известны из решения характеристического уравнения.
Определение двух неизвестных A и v производят и в этом случае по значениям iсв(0+) и iсв¢ (0+).
 |
Продифференцировав по времени уравнение (8.18), получим
Запишем уравнение (8.18а) при t = 0+:
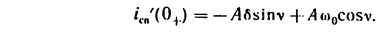 |
 |
Таким образом, для нахождения неизвестных A и v имеем два уравнения:
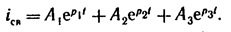 |
Для цепи, имеющей характеристическое уравнение третьей степени, свободный ток
 |
Найдем первую, а затем вторую производную от левой и правой частей уравнения (8.20):
 |
Запишем (8.20)—(8.22) при t == 0+:
Система уравнений (8.23) представляет собой систему трех линейных алгебраических уравнений с тремя неизвестными: A1, A2 и A3. Все остальные входящие в нее величины [p1, p2, p3, iсв(0+), iсв¢ (0+), iсв¢ ¢ (0+)] известны.
Сначала, пока еще не накоплено опыта в решении задач, для облегчения расчета величины и ее производной (производных) при t = 0+ рекомендуется решать задачу относительно тока через L или напряжения на C и только затем, используя законы Кирхгофа, определять любую другую величину через найденную.
|
|
