
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Трехфазная система э.д.с. Трехфазная цепь. Основные схемы соединения трехфазных цепей, определение линейных и фазных величин.
|
|
Трехфазная система ЭДС.
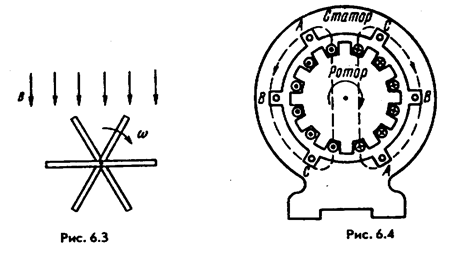
Под трехфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе на 120°. Графики их мгновенных значений изображены на рис. 6.1, векторная диаграмма — на рис. 6.2. Принцип получения трехфазной системы ЭДС иллюстрирует рис. 6.3. В равномерном магнитном поле с постоянной угловой скоростью вращаются три одинаковых жестко скрепленных друг с другом катушки.
Плоскости катушек смещены в пространстве друг относительно друга на 120°. В каждой катушке наводится синусоидальная ЭДС одинаковой амплитуды. По фазе ЭДС катушек сдвинуты на 120°.
Аналогичным путем можно получить двух- и четырехфазную 
систему ЭДС и более. Наибольшее практическое применение получила трехфазная система.
 |
ЭДС трехфазного генератора обозначают следующим образом: одну из ЭДС — ЕА, отстающую от нее на 120° ЭДС — ЁВ, а опережающую на 120° — ЁС. Последовательность прохождения ЭДС через одинаковые значения (например, через нулевое значение) называют последовательностью фаз.
Трехфазная цепь. Расширение понятия фазы.
Совокупность трехфазной системы ЭДС, трехфазной нагрузки (нагрузок) и соединительных проводов называют трехфазной цепью.
Токи, протекающие по отдельным участкам трехфазных цепей, сдвинуты относительно друг друга по фазе. Под фазой трехфазной цепи понимают участок трехфазной цепи, по которому протекает одинаковый ток. В литературе фазой иногда называют однофазную цепь, входящую в состав многофазной цепи. Под фазой будем также понимать аргумент синусоидально меняющейся величины. Таким образом, в зависимости от рассматриваемого вопроса фаза — это либо участок трехфазной цепи, либо аргумент синусоидально изменяющейся величины.
Основные схемы соединения трехфазных цепей, определение линейных и фазовых величин.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 |
Существуют различные способы соединения обмоток генератора с нагрузкой. Самым неэкономичным способом явилось бы соединение каждой обмотки генератора с нагрузкой двумя проводами, на что потребовалось бы шесть соединительных проводов. В целях экономии обмотки трехфазного генератора соединяют в звезду или треугольник. При этом число соединительных проводов от генератора к нагрузке уменьшается с шести до трех или до четырех.
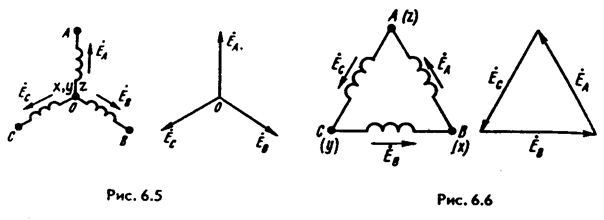
На электрической схеме трехфазный генератор принято изображать в виде трех обмоток, расположенных друг к другу под углом 120°. При соединении звездой одноименные зажимы (например, концы х, у, z.) трех обмоток объединяют в одну точку (рис. 6.5), которую называют нулевой точкой генератора О. Обмотки генератора обозначают буквами А, В, С; буквы ставят: А — у начала первой, В — у начала второй и С — у начала третьей фазы.
При соединении обмоток генератора треугольником (рис. 6.6) конец первой обмотки генератора соединяют с началом второй, конец второй — с началом третьей, конец третьей — с началом первой. Геометрическая сумма ЭДС в замкнутом треугольнике равна нулю. Поэтому если к зажимам А, В, С не присоединена нагрузка, то по обмоткам генератора не будет протекать ток.
Пять простейших способов соединения трехфазного генератора с трехфазной нагрузкой изображены на рис. 6.7 — 6.10.
 |
Точку, в которой объединены три конца трехфазной нагрузки при соединении ее звездой, называют нулевой точкой нагрузки и обозначают О'. Нулевым проводом называют провод, соединяющий нулевые точки генератора и нагрузки. Ток нулевого провода назовем I0. Положительное направление тока возьмем от точки О'
к точке О.
Провода, соединяющие точки А, В, С генератора с нагрузкой, называют линейными.
Схему рис. 6.7 называют звезда — звезда с нулевым проводом; схему рис. 6.8—звезда—звезда без нулевого провода; схему рис. 6.9, а — звезда — треугольник; схему рис. 6.9, б — треугольник — треугольник; схему рис. 6.10 — треугольник — звезда.
Текущие по линейным проводам токи называют линейными; их обозначают IA, IB, IC. Условимся за положительное направление токов принимать направление от генератора к нагрузке. Модули линейных токов часто обозначают IЛ (не указав никакого дополнительного индекса), особенно тогда, когда все линейные токи по модулю одинаковы.
 |
Напряжение между линейными проводами называют линейным и часто снабжают двумя индексами, например UAB (линейное напряжение между точками А и В); модуль линейного напряжения обозначают UЛ.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Каждую из трех обмоток генератора называют фазой генератора; каждую из трех нагрузок — фазой нагрузки; протекающие по ним токи—фазовыми токами генератора Iф или соответственно нагрузки, а напряжения на них — фазовыми напряжениями Uф.
Преимущества трехфазных систем.
Широкое распространение трехфазных систем объясняется главным образом тремя основными причинами:
1) передача энергии на дальние расстояния трехфазным током экономически более выгодна, чем переменным током с иным числом фаз;
2) элементы системы—трехфазный синхронный генератор, трехфазный асинхронный двигатель и трехфазный трансформатор — просты в производстве, экономичны и надежны в работе;
3) система обладает свойствами неизменности значения мгновенной мощности за период синусоидального тока, если нагрузка во всех трех фазах трехфазного генератора одинакова.
Расчет трехфазных цепей.
Трехфазные цепи являются разновидностью цепей синусоидального тока, и потому расчет и исследование процессов в них производят теми же методами и приемами, которые рассматривались в цепях однофазного синусоидального тока. Для цепей трехфазного тока применим также символический метод расчета и можно строить векторные, топографические и круговые диаграммы.
Аналитический расчет трехфазных цепей рекомендуется сопровождать построением векторных и.топографических диаграмм. Векторные диаграммы облегчают нахождение углов между токами и напряжениями, делают все соотношения более наглядными и помогают находить ошибки при аналитическом расчете, если последние возникнут.
Соединение звезда — звезда с нулевым проводом.
Если нулевой провод в схеме рис. 6.7 обладает весьма малым сопротивлением, то потенциал точки О' практически равен потенциалу точки О; точки О' и О фактически представляют собой одну точку. При этом в схеме образуются три обособленных контура, через которые проходят токи IA=EA/ZA, IB=EB/ZB, IC=EC/ZC
По первому закону Кирхгофа ток в нулевом проводе равен геометрической сумме фазовых токов:
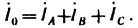
ЕслиZA=ZB=ZC(такую нагрузку называют равномерной), то ток I0 равен нулю и нулевой провод может быть изъят из схемы без изменения режима ее работы.
При неравномерной нагрузке фаз ток I0 в общем случае не равен нулю.
При наличии в нулевом проводе некоторого сопротивления расчет схемы производят методом узловых потенциалов.
Соединение нагрузки треугольником.
Выберем направление токов в фазах треугольника в соответствии с рис. 6.9, а.. Ток IABвызывается напряжением UAB. Модуль и фаза его относительно напряжения UABопределяются сопротивлением нагрузки ZAB. Ток IBC вызван напряжением UBC. Модуль и фаза его относительно UBCопределяются сопротивлением ZBC. Ток ICA вызван напряжением UCA и зависит от сопротивления ZCA. Линейные токи вычислим через фазовые токи по первому закону Кирхгофа:
 |
При равномерной нагрузке фаз линейные токи по модулю в √ З раз больше фазовых токов нагрузки. При неравномерной нагрузке линейные токи могут быть и больше и меньше фазовых токов нагрузки.
Оператор а трехфазной системы.
 |
Условимся комплексное число еj120˚ , по модулю равное единице, обозначать а и называть оператором трехфазной системы. Тогда
 |
Три вектора: I, a и a2 образуют симметричную трехфазную систему (рис. 6.15):
 |
Умножение какого-либо вектора на а поворачивает его без изменения модуля на угол 120° против часовой стрелки. Умножение вектора на а2 поворачивает его на угол 240° против часовой стрелки, или, что то же самое, поворачивает его по часовой стрелке на 120°.
С помощью оператора а можно выразить ЭДС Ев и Еc симметричной трехфазной системы через ЭДС Еа:
 |
Соединение звезда—звезда без нулевого провода.
На рис. 6.8 представлена схема с двумя узлами (точки О и О'). Для расчета токов в ней целесообразно пользоваться методом двух узлов. Напряжение между двумя узлами
 |
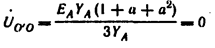 |
Если нагрузка равномерна (YA=YB=YC), то [см. соотношение (6.5)]
 |
и напряжение на каждой фазе нагрузки равно соответствующей ЭДС:
 |
Если нагрузка неравномерна, то U0'0≠ 0 и
 |
Токи в фазах нагрузки:
 |
Если в двух фазах нагрузка одинакова, например ZB=ZC≠ ZA, то формула (6.7) после преобразований имеет следующий вид:
2. Соотношения между линейными и фазными токами и напряжениями.
 |
При соединении генератора в звезду (см. рис. 6.7, 6.8, 6.9, а) линейное напряжение по модулю в √ 3 раз больше фазового напряжения генератора (Uф). Это следует из того, что Uл есть основание равнобедренного треугольника с острыми углами по 30°(рис. 6.11):
В основу формирования ряда трехфазных напряжений, когда последующее напряжение больше предыдущего в √ 3 раз, положен √ 3 = 1, 73. Приведем часть этого ряда при относительно низких напряжениях: 127, 220, 380, 660 В.
Линейный ток Iл при соединении генератора в звезду равен фазовому току генератора: Iл = Iф.
 |
 |
При соединении генератора в треугольник линейное напряжение равно фазовому напряжению генератора (см. рис. 6.6, 6.9, б):
При соединении нагрузки в звезду (см. рис. 6.7, 6.8, 6.10) линейный ток равен фазовому току нагрузки: Iл = Iф.
При соединении нагрузки треугольником положительные направления для токов выбирают по часовой стрелке. Индексы у токов соответствуют выбранным для них положительным направлениям: первый индекс отвечает точке, от которой ток утекает, второй — точке, к которой ток притекает.
 |
При соединении нагрузки треугольником (см. рис. 6.9, а, б) линейные токи не равны фазовым токам нагрузки и определяются через них по первому закону Кирхгофа:
Переходные процессы
|
|
