
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства линейных электрических цепей и методы их расчета.
|
|
ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА
Лекции
Содержание
Электрические цепи постоянного тока..…………………………… 3
Электрические цепи переменного тока…………………..………… 15
Электромагнитные устройства и трансформаторы………..… …….39
Электрические машины………..…………………………………...... 69
Электроника……………………………………………………………85
Электрические цепи постоянного тока
Свойства линейных электрических цепей и методы их расчета.
Определение линейных и нелинейных электрических цепей.
- Электромагнитное устройство с происходящими в нем и в окружающем его пространстве физическими процессами в теории электрических цепей заменяют некоторым расчетным эквивалентом—электрической цепью.
Электрической цепью называют совокупность соединенных друг с другом источников электрической энергии и нагрузок, по которым может протекать электрический ток. Электромагнитные процессы в электрической цепи можно описать с помощью понятий «ток», «напряжение», «э. д. с.», «сопротивление» (проводимость), «индуктивность», «емкость».
Постоянным током называют ток, неизменный во времени. Постоянный ток представляет собой направленное упорядоченное движение частиц, несущих электрические заряды.
Как известно из курса физики, носителями зарядов в металлах являются свободные электроны, а в жидкостях—ионы. Упорядоченное движение носителей зарядов в проводниках вызывается электрическим полем, созданным в них источниками электрической энергии. Источники электрической энергии преобразуют химическую, механическую и другие виды энергии в электрическую. Источник электрической энергии характеризуется величиной и направлением э. д. с. и величиной внутреннего сопротивления.
Постоянный ток принято обозначать буквой I, э. д. с. источника — E, сопротивление — R и проводимость — g. В Международной системе единиц (СИ) ток измеряют в амперах (А), э. д. с.—в вольтах (В), сопротивление — в омах (Ом) и проводимость — в сименсах (См).
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Изображение электрической цепи с помощью условных знаков называют электрической схемой (рис. 1.1, а).
Зависимость тока, протекающего по сопротивлению, от напряжения на этом сопротивлении принято называть вольт-амперной характеристикой (по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат—ток).
Сопротивления, вольт-амперные характеристики которых являются прямыми линиями (рис. 1.1, б), называют линейными сопротивлениями, а электрические цепи только с линейными сопротивлениями — линейными электрическими цепями.
Сопротивления, вольт-амперные характеристики(в. а. х.) которых не являются прямыми линиями (рис. 1.1, б), т. е. они нелинейны, называют нелинейными сопротивлениями, а электрические цепи с нелинейными сопротивлениями — нелинейными электрическими цепями.

Источник э. д. с. и источник тока.
Источник электрической энергии имеет э. д. с. Е и внутреннее сопротивление Rв. Если через него под действием э. д. с. Е протекает ток I, то напряжение на его зажимах U = E – I Rв при увеличении I уменьшается. Зависимость напряжения U на зажимах реального источника от тока I изображена на рис. 1.2, а.

Обозначим mu — масштаб по оси и, mi —масштабпо оси I. Тогда для произвольной точки на характеристике рис. 1.2,. а:
ab mu = I Rв; bc mi = I; tgα = ab/bc = Rв mi / mu.
Следовательно, tgα пропорционален Rв. Рассмотрим два крайних случая.
1. Если у некоторого источника внутреннее сопротивление Rв = 0, то вольт-амперная характеристика его будет в виде прямой (рис. 1.2, б). Такой характеристикой обладает идеализированный источник питания, называемый источником э. д. с.
Следовательно, источник э. д. с. представляет собой такой идеализированный источник питания, напряжение на зажимах которого постоянно (не зависит от тока) и равно э. д. с. Е, а внутреннее сопротивление равно нулю.
2. Если у некоторого источника беспредельно увеличивать э. д. с. Е и внутреннее сопротивление, то точка с (рис. 1.2, а.) отодвигается по оси абсцисс в бесконечность, а угол α стремится к 90" (рис. 1.2, в). Такой источник питания называют источником тока.
Следовательно, источник тока представляет собой идеализированный источник питания, который создает ток I=Ik, не зависящий от сопротивления нагрузки, к которой он присоединен, а его э. д. с. и внутреннее сопротивление равны бесконечности. Отношение двух бесконечно больших величин равно конечной величине — току Ik источника тока.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением Rв, заменяют расчетным эквивалентом. В качестве эквивалента может быть взят:
1) источник э. д. с. Е с последовательно включенным сопротивлением Rв равным внутреннему сопротивлению реального источника (рис. 1.3. а: стрелка в кпужке указывает направление возрастанияпотенциала внутри источника э.д. с.);
2) источник тока с током Ik = E/Rв и параллельно с ним включенным сопротивлением Rв, (рис. 1.3, б; стрелка в кружке указывает положительное направление тока источника тока).
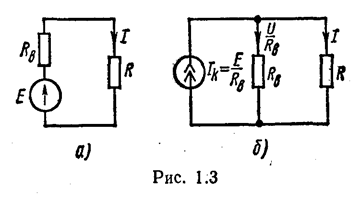 |
Ток в нагрузке (в сопротивлении R) для схем рис.1.3, а, б одинаков и равен I = E/(R+Rв), т. е. равен току для схемы рис. 1.1, а. Для схемы рис. 1.3, а это следует из того, что при последовательном соединении сопротивления R и Rв, складываются. В схеме рис. 1.3, 6 ток Ik = E/Rв, распределяется обратно пропорционально сопротивлениям R и Rв двух параллельных ветвей. Ток в нагрузке

Каким из двух расчетных эквивалентов пользоваться, совершенно безразлично. В дальнейшем используется в основном первый эквивалент. Обратим внимание на следующее:
1) источник э. д. с. и источник тока это идеализированные источники, физически осуществить которые, строго говоря, невозможно;
2) схема рис. 1.3, б эквивалентна схеме рис. 1.3, а в отношении энергии, выделяющейся в сопротивлении нагрузки, и не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника питания;
3) идеальный источник э. д. с. нельзя заменить идеальным источником тока.
Неразветвленные и разветвленные электрические цепи.
Электрические цепи подразделяют на неразветвлённые и разветвленные. На рис. 1.1, а представлена схема простейшей неразветвленной цепи. Во всех элементах ее течет один и тот же ток. Простейшая разветвленная цепь изображена на рис. 1.4, а; в ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рис. 1.4, б), то в этом месте есть электрическое соединение двух линий, в противном случае (рис. 1.4, в) его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым узлом.
 |
 |
Рис 1.4.
Напряжение на участке цепи.
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.
На рис. 1.5 изображен участок цепи, крайние точки которого обозначены буквами а и Ь. Пусть ток течет от точки а к точке Ь (от более высокого потенциала к более низкому). Следовательно, потенциал точки а выше потенциала точки Ь на величину, равную произведению тока на сопротивление:


В соответствии с определением напряжение между точками а и Ь

Следовательно, напряжение на сопротивлении равно произведению тока, протекающего по сопротивлению, на величину этого сопротивления.
В электротехнике разность потенциалов на концах сопротивления принято называть либо напряжением на сопротивлении, либо падением напряжения. В дальнейшем разность потенциалов на концах сопротивления.
Положительное направление падения напряжения на каком-либо участке (направление отсчета этого напряжения), указываемоена. рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению.
Рассмотрим вопрос о напряжении на участке цепи, содержащем не только сопротивление, но и э. д. с.

На рис. 1.6, а, б показаны участки некоторых цепей, по которым протекает ток. Найдем разность потенциалов (напряжение) между точками а и с для этих участков.
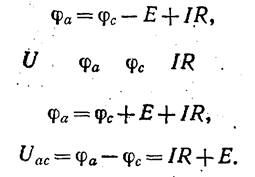 для 1.6. а
для 1.6. а
для 1.6. б
Положительное направление напряжения иас показывают стрелкой от а к с.
|
|
