Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение и моделирование отрасли (на основе численной модели сельского хозяйства)
|
|
Рассматривается сельско –хозяйственная отрасль, включающая четыре предприятия, выпускающих два вида продукции. Экономические показатели производства представлены в табл. 5.3.
Таблица 5.3.
Экономические показатели отрасли сельского хозяйства
| № | Объём продукции, тыс. кг. | Производитель | Продукция (1 кг.) | ||
| Стоимость руб. | Затраты руб. | Прибыль руб. | |||
| Соевое масло х 1 Измельченная соя х 2 | «ОАО ДАК» | ||||
| Гречневая крупа х 3 Гречневая крупа быстрого приготовления х 4 | «ООО МЕГАДВ» | ||||
| 4 6 | Рис длиннозерный х 5 Рисовая мука х 6 | «ООО МИКС» | |||
| Картофель х 7 Картофель для микроволновой печи х 8 | «ООО ПримАГРО» |
На основе маркетинговых исследование условно выделили 4 группы потребителей: пенсионеры, студенты, дети, работающее население. Каждая группа потребляет два вида продуктов – (1, 5), вторая –(2, 6), третья – (3, 7), четвертая – (4, 8).
Связь спроса и предложения решена следующим образом.
Спрос определяется: максимальной суммой, которую могут выделить четыре группы потребителей в тыс. руб. на свои покупки b 
=14000, b 
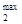=19000, b 
=16500, b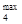 
=19000; минимальной суммой, которая необходима для наименьшего потребления своего продукта b 
=8000, b 
=11000, b 
=11000, b 
=12000.
Предложение определяется тем, какой объем финансовых средств в тыс. руб. фирма может выделить для изготовления своей продукции b 1=14000, b 2=19000, b 3=16500, b 4=19000.
Модель может быть использована при других взаимоотношениях спроса и предложения.
Требуется построить оптимизационную модель рынка и рассчитать объемы спроса и предложения
Построение модели рынка. В качестве неизвестного примем вектор X ={ xj, j = 
}, каждая компонента которого характеризует объем продукции произведенной и потребляемой рынком. Соответствие названия продукта и переменной представлено в табл. 5.3. Математическая модель отраслевого рынка (5.5.1)-(5.5.8) с четырьмя потребителями и производителями (модель 4*4) представим в виде векторной задачи линейного программирования
opt F (X)={ max F 1(X)={ max f 1(X) = 25 x 1 + 25 x 2, (5.5.9)
max f 2(X) = 30 x 3+ 25 x 4, (5.5.10)
max f 3(X) = 23 x 5 + 30 x 6, (5.5.11)
max f 4(X) = 20 x 7+ 16 x 8}, (5.5.12)
min F 2(X)={ min f 5(X) = 60 x 1 + 65 x 5 , (5.5.13)
min f 6(X) = 50 x 2+ 75 x 6, (5.5.14)
min f 7(X) = 70 x 3 + 35 x 7 , (5.5.15)
min f 8(X) = 50 x 4+ 40 x 8}}, (5.5.16)
при ограничениях 8000 ≤ 60 x 1 + 65 x 5 ≤ 14000, (5.5.17)
11000 ≤ 50 x 2+ 75 x 6 ≤ 19000 (5.5.18)
10000 ≤ 70 x 3 + 35 x 7 ≤ 16500, (5.5.19)
12000 ≤ 50 x 4 + 40 x 8≤ 19000, (5.5.20)
35 x 1+ 25 x 2 ≤ 14000, (5.5.21)
40 x 3+ 25 x 4 ≤ 19000, (5.5.22)
42 x 5+ 45 x 6 ≤ 16500, (5.5.23)
15 x 7+ 24 x 8 ≤ 19000, (5.5.24)
x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8 ³ 0. (5.5.25)
Решение задачи линейного программирования (5.5.9)-(5.5.25) покажем в системе Matlab в соответствии с алгоритмом решения ВЗЛП на основе нормализации критериев и принципа гарантированного результата. Алгоритм представим как последовательность шагов.
Шаг 1, 2. Решение по каждому критерию: наилучшее, наихудшее.
Решение по первому критерию представляет обращение к функции linprog, решающей задачу линейного программирования
В результате решения получим.
Критерий 1 - оптимальные значения переменных:
X 
= X1max ={ x 1=250.67, x 2=276.30, x 3=37.17, x 4=31.25};
оптимальное значение целевой функции: наилучшее
f = f 1 max =27730.0, наихудшее f 
= f 1 min = 2100.0.
Аналогично по остальным критериям.
Критерий 2. X 
= X 2 max ={ x 1=24 x 2=20 x 3=210.2 x 4=441.3},
f = f 2 max = 27029, f 
= f 2 min = 1780.
Критерий 3. X 
= X 3 min ={ x 1=134.2 x 2=179.8 x 3=30.27 x 4=120}
f = f 3 min =19000, f 
= f 3 max = 33000.
Критерий 4. X 
= X 4 min ={ x 1=103 x 2=138.4 x 3=121.9 x 4=71.9}
f = f 4 min =22000, f 
= f 4 max = 35500.
Шаг 2. Выполняется анализ критериев в ВЗЛП, для чего в оптимальных точках X 
, X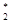 
определяются величины целевых функций F (X*)={{ fq (X 
), k= 
}, q= } и относительных оценок l(X*)={{l q (X ), k= }, q= }.
F(X*)=f= 
= 
,
Определяются отклонения dk=f -f 
, k= 
: D = [ d 1=25630 d 2=25249 d 3=-14000 d 4=-13500]; относительные оценки l k (X)=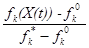 
, k= .
l (X*) =L= 
= 
,
Шаг 4. Строится и решается l-задача.
lo = max l,
при ограничениях:
l - (25 x 1 + 25 x 2 - f )≤ 0, l - (30 x 3+ 25 x 4 - f )≤ 0,
l - (23 x 5 + 30 x 6 - f )≤ 0, l - (20 x 7+ 16 x 8 - f )≤ 0}, (5.5.26)
l - (60 x 1 + 65 x 5 - f )≤ 0, l - (50 x 2+ 75 x 6 - f )≤ 0,
l - (70 x 3 + 35 x 7 - f )≤ 0, l - (50 x 4+ 40 x 8 - f )≤ 0, (5.5.27)
8000 ≤ 60 x 1 + 65 x 5 ≤ 14000, 11000 ≤ 50 x 2+ 75 x 6 ≤ 19000, 10000 ≤ 70 x 3 + 35 x 7 ≤ 16500, 12000 ≤ 50 x 4 + 40 x 8≤ 19000, (5.5.28)
35 x 1+ 25 x 2 ≤ 14000, 40 x 3+ 25 x 4 ≤ 19000,
42 x 5+ 45 x 6 ≤ 16500, 15 x 7+ 24 x 8 ≤ 19000, (5.5.29)
x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8 ³ 0. (5.5.30)
Результаты решения l-задачи: оптимальные значения переменных: Xo = { x 1= 0.4368, x 2=218.94, x 3 =42.703, x 4=20.0, x 5=326.37};
оптимальное значение целевой функции: l o = 0.4368.
Проверка. В результате решения получим:
f 1(Xo)= 13296, f 2(Xo)= 12810, f 3(Xo)=26884, f 4(Xo)=29603,
l1(Xo)= 0.4368, l2(Xo)= 0.4368, l3(Xo)= 0.4368, l4(Xo)= 0.4368,
т. е. lo£ l k (Xo), k =1, 2.
Эти результаты показывают, что в точке Xo оба критерия в относительных единицах достигли уровня l o = 0.4368. Любое увеличение одного из критериев выше этого уровня приводит к уменьшению другого критерия, т.е. точка Xo оптимальна по Парето.
|
|