Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение модели отрасли
|
|
Математическую модель одно - продуктового рынка (5.4.1)-(5.4.5) можно рассматривать как модель отрасли:
opt F (X (t))= { F 1(X (t)) = { max fq (X (t)) = 
pqxql (t), q= 
}, (5.5.1)
F 2(X (t))={ min fl (X (t)) = 
pqxql (t), l= 
}}, (5.5.2)
{ F 3(X (t)) = { max få q (X (t)) = pqxql (t), (5.5.3)
min få l (X (t)) = pqxql (t), l= }}, (5.5.4)
b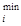 
£ pqxql (t)£ b 
(t)+Δ b (t+ Δ t), l= , (5.5.5)
aqxql (t)£ bq (t)+Δ bq (t+ Δ t), q= , (5.5.6)
p 
£ pq £ p 
, (5.5.7)
xql(t) ³ 0, q= , l= , (5.5.8)
где F (X (t)) - векторный критерий, в котором K = Q È L È 2 - множество критериев - производителей Q, потребителей L и два системных критерия (5.5.3)-(5.5.4), характеризующих отрасль в целом;
в (5.5.1) F 1(X (t))- векторный критерий Q производителей, которые максимизируют прибыль от производства и продажи отдельного вида товаров;
в (5.5.2) F 2(X (t))- векторный критерий L потребителей, которые минимизируют свои затраты, за счет стоимости на покупаемую продукцию;
xql, q= , l= - управляющие переменные представляющие объем производства и последующих продаж;
pq = pq - aq, q= - прибыль производителей, определяющаяся разностью между ценой продажи pq и затратами aq;
(5.5.5) - ограничения по бюджетным (финансовым) возможностям L потребителей, Δ b (t+ Δ t) прирост бюджетных возможностей у потребителей на очередной плановый период;
(5.5.6) - ограничения по производственным мощностям Q производителей, Δ bq (t+ Δ t) прирост инвестиций в производство q -го предприятия отрасли на период Δ t;
(5.5.7) - ограничения, определяющие пределы изменения стоимости единицы товара, установленные на рынке, если p = p , то задача (5.5.1)-(5.5.8) линейная, иначе нелинейная;
(5.5.8) - ограничения, связанные с не отрицательностью объемов произведенной и проданной продукции.
Задача (5.5.1)-(5.5.8) представляет модель отраслевого рынка на дискретный период t Î T.
Для решения векторной задачи математического программирования (5.5.1)-(5.5.8) используются методы, основанные на нормализации критериев и принципе гарантированного результата, которые дают возможность решать задачи при равнозначных критериях и заданном приоритете критерия, представленные в девятой главе.
Конец
|
|