Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение модели рынка монопсонии
|
|
Для анализа рыночной структуры монопсонии рассмотрим представленную модель, когда на рынке с одним товаром (две модификации) действуют два производителя и один потребитель этого продукта, хотя модель позволяет анализировать и более крупные.
Дано. Числовые данные аналогичны модели олигополии. Но в этой задаче будет один два производителя, выпускающих продукты.
Взаимосвязь спроса и предложения решена аналогично, как и для модели олигополии, т. е. в модели (5.4.6)-(5.4.10) с предлагаемыми числовыми параметрами, предложение превышает спрос, хотя модель может быть использована и при других взаимоотношениях спроса и предложения.
Построить оптимизационную модель рынка монопсонии и рассчитать объемы спроса-предложения.
Построение математической модели рынка - монопсонии с одним производителем и двумя потребителями в виде векторной задачи линейного программирования представим следующим образом:
opt F (X)={ max f 1(X) =10 x 1+10 x 2, max f 2(X)=10 x 3+10 x 4, (5.4.36)
min f 3(X) = 50 x 1 + 50 x 2+ 60 x 3+ 60 x 4}, (5.4.37)
при ограничениях
7000 ≤ 50 x 1+ 50 x 2+60 x 3 +60 x 4 ≤ 10000, (5.4.38)
40 x 1+ 40 x 2 ≤ 5000, 50 x 3+ 50 x 4 ≤ 5000, (5.4.39)
x 1, x 2, x 3, x 4 ³ 0. (5.4.40)
Исследование модели монопсонии, представленной в виде векторной задачи (5.4.36)-(5.4.40), проведем с учетом целенаправленности двух производителей и одного потребителя.
Решение векторной задачи (5.4.36)-(5.4.40) при равнозначных критериях.
Шаг 1, 2. Решаем задачу (5.4.36)-(5.4.40) по каждому критерию.
Сначала для двух производителей предоставляются наиболее благоприятные условия, т. е. при оптимизации учитываются только их целенаправленность и ограничения, накладываемые на их производственную деятельность, в результате решения получим оптимальные объемы продукции, которые в принципе может выпустить первый и второй производитель, - X 
, X 
с соответствующей прибылью f =f 1(X ), f =f 2(X ):
X ={ x 1=62.5, x 2=62.5, x 3=0.4487, x 4=60.8435}, f 1(X )=1250,
X 
={ x 1=10, x 2=10, x 3=50, x 4=50}, f 1(X )=200.
X ={ x 1=30.98, x 2=30.98, x 3=50, x 4=50}, f 2(X )= 1000,
X 
={ x 1=62.5, x 2=62.5, x 3=6.25, x 4=6.25}, f 2(X )= 125.
Создаются благоприятные условия для потребителя, т. е. решается векторная задача (5.4.36)-(5.4.40) с критерием (5.4.37). В результате решения получим точку оптимума X 
и соответственно f3(X ):
X ={ x 1=35.28, x 2=35.28, x 3=28.93, x 4=28.93}, f 3(X )=7000,
X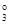 
={ x 1=51.3165, x 2=51.3165, x 3=40.5696, x 4=40.5696}, f 3(X )=10000.
Шаг 3. Выполняется стандартная нормализация критериев и анализ оптимальных результатов решения, полученных по каждому критерию:
f * = f 1(X )=1250.0 f 2(X )=612.9 f 3(X )=9927.5
f 1(X )=619.7 f 2(X )=1000.0 f 3(X )=9098.6
f 1(X )=705.6 f 2(X )=578.6 f 3(X )=7000.0.
l* = l1(X )=1.0000 l2(X )=0.5576 l3(X )=0.0242
l1(X )=0.3997 l2(X )=1.0000 l3(X )=0.3005
l1(X )=0.4815 l2(X )=0.5185 l3(X )=1.0000
Шаг 4. Построение l-задачи. Она по своей структуре аналогична задаче (5.4.26)-(5.4.30).
Решение l-задачи.
l o = 0.6111, Xo ={ x 1=42.0833, x 2=42.0833, x 3= 32.9861, x 4= 32.9861}.
f 1(Xo) =841.7, l1(Xo) =0.6111,
f 2(Xo) =659.7, l2(Xо) =0.6111,
f 3(Xo) =8166.7, l3(Xo) =0.6111.
r 1 =8166.7, r 2=3366.7, r 3=3298.6.
Точка Xo оптимальна по Парето - любое улучшение (увеличение) одного из них приводит к ухудшению другого.
Моделирование рынка - монопсонии при приоритете потребителей.
Решаем векторную задачу (5.4.36)-(5.4.40) при заданном приоритете второго и третьего критерия (потребителей) над первым критерием (производителем). Задаем вектор приоритетов P 1={ p 
=1, p 
=1, p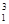 
=1.3512}, который вставляется в l-задачу. В результате решения l-задачи при заданных приоритетах критериев получаем точку оптимума Xo, fk (Xo), k = 
и максимальную относительную оценку l o.
l o = 0.6486, Xo ={ x 1=44.05, x 2=44.05, x 3=34.31, x 4=34.31}.
f 1(Xo) =881.0, l1(Xo) =0.6486,
f 2(Xo) =692.5, l2(Xo) =0.6486,
f 3(Xo) =856.0, l3(Xo) =0.4800.
lo = p l1(Xo)=l2(Xo)=l3(Xo)=0.6486,
Моделирование рынка-монопсонии при приоритете производителя.
Решается векторная задача (5.4.36)-(5.4.40) при заданном приоритете первого критерия над вторым и третьим критерием (потребителями).
Задается вектор приоритетов P 1={ p =1.3512, p =1.3512, p 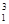=1}, который вставляется в l-задачу. В результате решения l-задачи при заданных приоритетах критериев получаем точку оптимума Xo, fk (Xo), k= 
и максимальную относительную оценку l o.
l o = 0.7660, Xo ={ x 1=39.76, x 2=39.76, x 3=31.05, x 4=31.05}.
f 1(Xo) =795.2, l1(Xo) = 0.5669,
f 2(Xo) =621.0, l2(Xo) = 0.5669,
f 3(Xo)=7702.1, l3(Xo) = 0.766.
l o = p l1(Xo) = l2(Xo) = l3(Xo) = 0.766.
Полученный результат решения совпадает с моделью олигополии.
|
|