Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Удаление элемента из дерева двоичного поиска

Алгоритм удаления элемента из дерева зависит от расположения этого элемента в дереве и включает в себя четыре ситуации:

1. Элемента со значением, равным х, нет.

2. Элемент со значением х является терминальным узлом.

3. Элемент со значением х имеет одного потомка.

4. Элемент со значением х имеет двух потомков.

При удалении листа или элемента, имеющего одного потомка, сложности нет. Действия аналогичны удалению элемента в линейном списке.

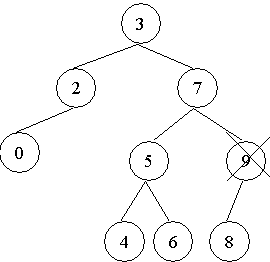
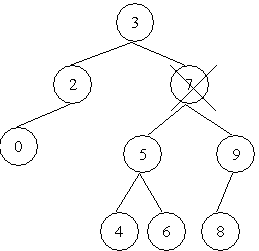
	Если элемент имеет двух потомков, то одной ссылкой нельзя указать на два направления. В этом случае удаляемый элемент необходимо заменить. Для замены выбирается самый правый элемент его левого поддерева или самый левый элемент его правого поддерева (6 или 8 – это ближайшие элементы по значению к удаляемому элементу).

Алгоритм удаления элемента

Алгоритм включает в себя четыре ситуации, рассмотренные выше.

Ситуация 1: Удаляемый узел не найден.

Действия: Алгоритм удаления заканчивает работу.

Ситуация 2: Узел не имеет потомков, т.е. является листом.

Действия: Обновить его родительский узел так, чтобы его поддерево оказалось пустым.

Ситуация 3.1: Узел имеет левого потомка, но не имеет правого.

Действия: Присоединить левое поддерево узла к его родителю.

Ситуация 3.2: Узел имеет правого потомка, но не имеет левого.

Действия: Присоединить правое поддерево узла к его родителю.

Ситуация 4: Удаление узла с двумя потомками.

Действия: Необходима замена удаляемого узла.

Выберем для замены самый правый узел левого поддерева.

Определим следующее:

D - удаляемый узел;

Р - родитель удаляемого узла;

R - заменяющий узел;

PR - родитель узла R.

1. Перейти к левому поддереву узла D, потому что заменяющий узел R меньше, чем удаляемый узел D.

2. Заменяющий узел R является максимальным узлом левого поддерева узла D. Спускаемся по правому поддереву и ищем заменяющий узел R. Во время спуска следим за предшествующим узлом PR. При этом возможны два случая:

2.1. Правое поддерево пусто. Заменяющий узел R является левым сыном удаляемого узла. PR соответственно указывает на удаляемый узел D. Тогда выполняем следующие действия:

2.1.1. Присоединяем правое поддерево узла D в качестве правого поддерева к узлу R;

2.1.2. Родителя P удаляемого узла присоединяем к R.

2.2. Правое поддерево не пусто. Тогда заменяющий узел будет или листовым узлом или узлом, имеющим только левое поддерево. В любом случае выполняем следующие действия:

2.2.1. Отсоединить узел R от дерева.

2.2.2. Потомков узла R присоединить к его родительскому узлу PR (Левое поддерево R присоединяется в качестве правого поддерева к PR).

2.2.3. Удаляемый узел D заменяется узлом R: наследники узла D присоединяются в качестве наследников к узлу R, узел R присоединяется к родительскому узлу Р.

3.4. Бинарные деревья, представляемые массивами

Если данные бинарного дерева хранятся в элементах массива, то к данным может использоваться прямой доступ. Нулевой элемент массива – это корень дерева. Для каждого узла A [ i ] в n -элементном массиве индекс его наследников вычисляется по следующим формулам:

Индекс левого наследника равен 2* i +1.

Индекс правого наследника равен 2* i +2.

Индекс родителя можно вычислить по следующей формуле:

Индекс родителя равен (i -1)/2.

Представление дерева с использованием массивов удобно использовать для законченного бинарного дерева. Но при хранении дерева с небольшой плотностью в массиве имеются неиспользуемые элементы, что вызывает некоторые проблемы при работе с массивом.

Например:

	Законченное бинарное дерево: int A[]={5, 1, 3, 9, 6, 2, 4, 7, 0, 8};
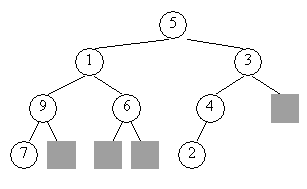
	Бинарное дерево с меньшей плотностью: int A[]={5, 1, 3, 9, 6, 4, #, 7, #, #, #, 2};