Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Структура двоичного дерева

Существует два пути представления двоичного дерева в памяти компьютера:

1. Последовательное представление с использованием обычного массива.

2. Представление в виде динамической структуры.

При последовательном представлении дерева с использованием массива двоичное дерево упаковывается в одномерный массив.

Это представление использует только один линейный массив - TREE.

Корень дерева находится в первом элементе массива TREE [0], две дочерние вершины - в соседних элементах и т.д.

Если узел n занимает элемент массива TREE [ K ], то его левая дочерняя вершина сохранена в TREE [2 K +1], а правая дочерняя вершина - в TREE [2 K +2].

Недостатки:

· размер дерева ограничен размером массива;

· для хранения дерева с небольшой плотностью требуется массив, б о льшая часть которого может оказаться неиспользуемой.

При реализации двоичных деревьев чаще всего используются динамические структуры данных.

Структура дерева может быть представлена следующим образом:

struct TREE{
int dann;
TREE *pleft;
TREE *pright;
};

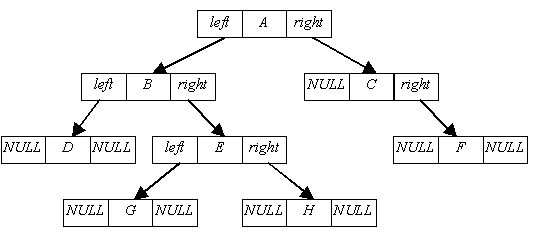
Каждый узел дерева содержит поле данных и два поля с указателями. Поля указателей называются левым указателем и правым указателем, потому что они указывают на левое и правое поддерево соответственно.

Листовой узел содержит NULL в поле правого и левого указателей.

Допустим, необходимо построить дерево с n узлами и минимальной высотой. Для этого нужно располагать максимально возможное число узлов на всех уровнях, кроме самого нижнего.

Идеально сбалансированное дерево – это дерево с максимально возможным числом узлов на всех уровнях, кроме самого нижнего.

В идеально сбалансированном дереве для каждого узла число узлов в левом и правом поддеревьях различаются не более чем на 1.

Алгоритм построения идеально сбалансированного дерева при известном числе узлов n:

1. Взять один узел в качестве корня.

2. Построить левое поддерево с nl = n /2 узлами при помощи этого же алгоритма.

3. Построить правое поддерево с nr = n - nl -1 узлами при помощи этого же алгоритма.

Пример

Для последовательности чисел - 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 - идеально сбалансированное дерево будет иметь следующий вид: