Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Включение в сбалансированное дерево

Преимущество AVL -деревьев состоит в их сбалансированности, которая поддерживается соответствующими алгоритмами вставки-удаления.

Процесс включения является почти таким же, как и для бинарного дерева поиска. Осуществляется рекурсивный спуск по левым и правым наследникам, пока не встретится пустое поддерево, а затем производится пробное включение нового узла в этом месте.

1. Следовать по пути поиска, пока не окажется, что ключа нет в дереве.

2. Включить новый узел и определить новый показатель сбалансированности.

3. Пройти обратно по пути поиска и проверить показатель сбалансированности у каждого узла.

Возможны три ситуации: в первых двух узел сохраняет сбалансированность и реорганизация поддеревьев не требуется, а нужно лишь скорректировать показатель сбалансированности данного узла. В третьем случае разбалансировка дерева требует одинарного или двойного поворотов узлов.

Случай 1. Узел на поисковом маршруте изначально является сбалансированным (balance равен 0). После включения в поддерево нового элемента узел стал перевешивать влево или вправо, в зависимости от того, в какое поддерево было произведено включение. Если элемент был включен в левое поддерево, показателю сбалансированности присваивается -1, а если в правое, - то 1.

До включения узла 55

После включения узла 55

Случай 2. Одно из поддеревьев узла перевешивает, и новый узел включается в более легкое поддерево. Узел становится сбалансированным.

До включения узла 55

После включения узла 55

Случай 3. Одно из поддеревьев узла перевешивает, и новый узел включается в более тяжелое поддерево. Тем самым нарушается условие сбалансированности, так как balance выходит за пределы -1... 1. Чтобы восстановить равновесие, нужно выполнить поворот.

Повороты

Повороты необходимы, когда родительский узел P становится разбалансированным. Фактически ссылки обмениваются значениями по кругу, что приводит к однократному или двукратному повороту двух или трех узлов. Кроме вращения ссылок, следует также изменить соответствующие показатели сбалансированности узлов.

Одинарный поворот вправо происходит тогда, когда родительский узел P и его левый потомок LC начинают перевешивать влево после включения узла в позицию X. В результате такого поворота LC замещает своего родителя, который становится правым наследником. Бывшее правое поддерево узла LC (ST) присоединяется к P в качестве левого поддерева. Это сохраняет упорядоченность, так как узлы в ST больше или равны узлу LC, но меньше узла P. Поворот уравновешивает как родителя, так и его левого потомка.

Пример:

Исходное дерево	Показатели сбалансированности до поворота
После поворота	Попытка включить узел 5 в AVL -дерево нарушает AVL -условие для узла 30 и выводит его из равновесия. Одновременно левое поддерево узла 15 (LC) становится перегруженным. Для переупорядочения узлов вызывается одинарный поворот вправо. В результате родительский узел (30) становится сбалансированным, а узел 10 - перевешивающим влево.

Двойной поворот вправо происходит тогда, когда родительский узел (P) становится перевешивающим влево, а его левый потомок (LC) - перевешивающим вправо. NP - корень правого перевешивающего поддерева узла LC. Тогда в результате поворота узел NP замещает родительский узел.

Возможны два варианта:

Вставка узла в левое поддерево узла NP
Вставка узла в правое поддерево узла NP

Пример:

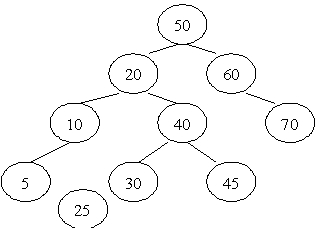
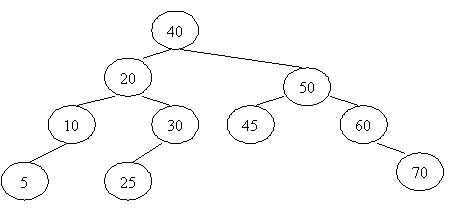
Попытка включить узел 25 разбалансирует корневой узел 50. В этом случае узел 20 (LC) приобретает слишком высокое правое поддерево и требует двойной поворот. Новым родительским узлом (NP) становится узел 40. Старый родительский узел становится его правым наследником и присоединяет к себе узел 45, который также переходит с левой стороны дерева.