Деревья двоичного поиска

Деревья двоичного поиска широко распространены в программировании.

Значение содержимого каждой вершины дерева двоичного поиска:

1) больше или равно, чем содержимое любой из вершин его левого поддерева;

2) меньше, чем содержимое любой из вершин его правого поддерева.

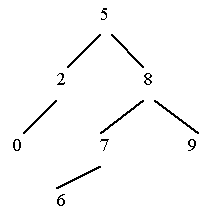
Распространенность деревьев двоичного поиска в программировании является следствием эффективности методов поиска в этих деревьях.

Для линейных структур сложность алгоритма последовательного поиска равна O (n), где n – это количество элементов структуры.

Для законченного бинарного дерева сложность алгоритма поиска равна .

Например, в списке из 10 000 элементов максимальное число сравнений при последовательном поиске равно 10 000.

Поиск на законченном дереве потребовал бы не более 14-ти сравнений.

Алгоритм вставки элемента в дерево двоичного поиска (просмотр дерева всегда начинается с его корня):

1. Значение, помещаемое в дерево, сравнивается со значением текущего узла.

2. Если значение, помещаемое в дерево, меньше значения текущего узла, то проверяется следующее:

a. если у текущего узла слева нет наследников, то прикрепляем узел со значением в качестве левого наследника;

b. иначе спускаемся по левой ветви дерева на уровень ниже

3. Если значение, помещаемое в дерево, больше или равно значению текущего узла, то проверяется следующее:

a. если у текущего узла справа нет наследников, то прикрепляем узел со значением в качестве правого наследника;

b. иначе спускаемся по правой ветви дерева на уровень ниже.

3.3. Операции с двоичными деревьями