Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Критерий Манна-Уитни.

Этот критерий был разработан для тех же целей, что и критерий Вилкоксона. Имеются две выборки. Требуется проверить однородность, т.е. можно ли считать, что эти выборки из одной и той же популяции. Для критерия Манна-Уитни требуется, чтобы шкала проверяемого признака была, как минимум, порядковая (интервальную шкалу тоже можно использовать).

Обозначим размер первой выборки m, а второй – n. Мы можем сравнить любой элемент первой выборки с любым элементом второй выборки (порядковая шкала позволяет это сделать). Будем называть успехом ситуацию, когда элемент первой выборки оказался больше элемента второй выборки. Ситуацию, когда он оказался меньше, назовем неудачным исходом. Наконец, для определенности будем считать, что случаев равенства у нас нет. Если случаи равенства имеются, то можно каждые два случая равенства заменять одним успехом и одной неудачей.

Если сравнить каждый элемент 1-й группы с каждым элементом 2-й группы, у нас окажется m·n парных сравнений. Общее количество успехов обозначим буквой U. В случае, когда популяция однородна (т.е. значение элемента не зависит от того, к какой из выборок он относится), в любом сравнении получить «успех» или «неудачу» можно с равной вероятностью. Поэтому в среднем у нас из всех m*n сравнений будет появляться (m·n/2) «успехов» и (m·n/2) «неудач». В действительности имеет место статистический разброс, поэтому мы даже при наличии однородности, скорее всего, получим экспериментальное значение U, большее или меньшее, чем (m·n/2). Осталось выяснить, насколько значимо такое отклонение.

Выбираем уровень значимости (например, α =0, 05 или α =0, 01). По специальной таблице критерия Манна-Уитни (см. Приложение 6) находим теоретическое значение U_теор. Если оказывается, что 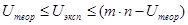, то популяцию можно считать однородной. Если неравенство не выполняется (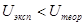, либо 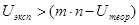), то гипотеза об однородности отвергается, при этом считается, что значения проверяемого признака зависят от того, в какой группе находится респондент.

Вычислим, для примера, значение критерия Манна-Уитни для задачи, рассмотренной в рассказе о критерии Вилкоксона. Имелись две группы данных, в первой группе значения 3, 4, 6, 10, 13, 17 (всего 6 значений), во второй группе - 1, 2, 5, 7, 16, 20, 22 (7 значений). Сравниваем первое значение из 1-й группы со всеми значениями из 2-й группы. Имеем только 1 успех (3> 2). Для второго значения (числа 4) – тоже 1 успех, для третьего (6) – 2 успеха, для числа 10 – 3 успеха, и т.д. Суммируем число успехов и получаем: U_эксп=1+1+2+3+3+4=14.

Теперь выберем α (например, α =0, 05) и определим для него по таблице из Приложения 6 значение U_теор.. Смотрим на пересечении столбца с m=6 и строки с n=7, что U_теор=6. Находим также, что 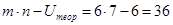. Поскольку значение U_эксп=14 больше 6, но меньше 36, мы принимаем гипотезу об однородности и считаем выборки взятыми из одной и той же популяции.

Как Вы уже, возможно, обратили внимание, при вычислениях статистики Манна-Уитни для каждого i-го элемента (из m элементов) 1-й группы мы получаем некоторое число успехов, которое зависит от того, сколько элементов из 2-й группы оказалось больше него. Если проделать операцию, описанную в критерии Вилкоксона, т.е. расположить объединенную выборку в порядке возрастания, то справа от i-го элемента расположится столько элементов, сколько «успехов» дает этот элемент при вычислении критерия Манна-Уитни. Поэтому величины критериев Вилкоксона и Манна-Уитни связаны между собой, а критерии проверяют одни и те же закономерности.