Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коэффициент линейной корреляции Пирсона
|
|
Коэффициент линейной корреляции Пирсона R служит для измерения силы связи двух признаков, каждый из которых измеряется по интервальной шкале. В остальном его свойства схожи с коэффициентами ранговой корреляции. Диапазон его изменения - от -1 до 1, притом значение ~0 означает отсутствие связи между ответами на изучаемые вопросы (т.е. то, что признаки независимы). Значение R~1 означает, что чем больше у респондента значение 1-го фактора, тем больше у него ожидаемое значение 2-го фактора. Наоборот, R~ -1 означает, что чем больше значение 1-го фактора, тем меньше ожидаемое значение 2-го фактора.
Рассмотрим вычисление коэффициента корреляции на следующем примере. Пусть студенты сдавали математику и информатику и получили следующие оценки:
| Оценка по математике | |||||||||
| Оценка по информатике |
Требуется проверить, связаны ли оценки по математике и информатике.
Коэффициент корреляции Пирсона вычисляется по следующей формуле:
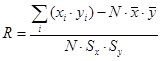
Здесь xi и yi – ответы i-го респондента на 1-й и 2-й вопросы, соответственно,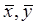 
- средние значения, а Sx и Sy – стандартные отклонения.
Для вычисления коэффициента корреляции сначала требуется вычислить средние значения. Вычисляем:
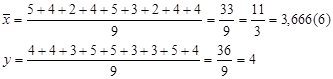
Также требуется вычислить стандартные отклонения. Вычисляем:
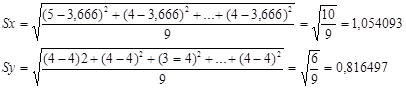
На следующем этапе находим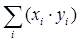 
. Эта сумма равна:
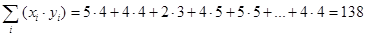
Подставляем найденные величины в формулу и получаем:
|
|
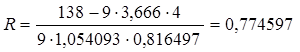