
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение линейной регрессии
|
|
Уравнение линейной регрессии – это уравнение прямой линии 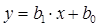 , описывающее зависимость ожидаемых значений одной случайной величины (Y) от значений другой случайной величины (X). Предполагается, что связь между величинами линейная. Если мы знаем уравнение линейной регрессии, то по ответу человека на вопрос X мы можем спрогнозировать (с некоторой точностью) его ответ на вопрос Y.
, описывающее зависимость ожидаемых значений одной случайной величины (Y) от значений другой случайной величины (X). Предполагается, что связь между величинами линейная. Если мы знаем уравнение линейной регрессии, то по ответу человека на вопрос X мы можем спрогнозировать (с некоторой точностью) его ответ на вопрос Y.
Коэффициент b1 в уравнении регрессии с математической точки зрения имеет смысл тангенса угла наклона прямой Y(x), а с другой стороны, имеет смысл коэффициента корреляции Пирсона, нормированного на величины стандартных отклонений: 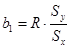
Вычислим его для примера про оценки по математике и информатике:
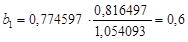
Коэффициент b0 имеет смысл значения y в точке пересечения оси y (при х=0). Его можно найти, если подставить в уравнение регрессии значение b1 и средние значения: 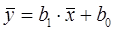
Вычисляем: 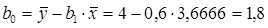
Итак, для нашего примера уравнение регрессии имеет вид 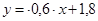 .
.
Некоторые свойства уравнения регрессии проиллюстрируем на графиках:
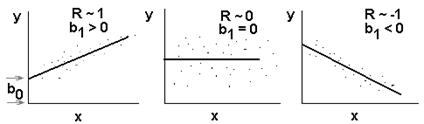
|
|
