
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коэффициент контингенции. Кэффицент Юла. Коэффициенты детерминации.
|
|
Для данной задачи требуется два вопроса, каждый из которых измеряется по дихотомической шкале, то есть имеет только два фиксированных варианта ответа. Для простоты мы будем считать, что эти варианы ответа - «Да» и «Нет». Нетрудно понять, что другие варианты ответа (например, «белый» и «черный») можно тоже свести к ответам «да» и «нет» («да, является белым» и «нет, не является белым»). Всех респондентов, ответивших на два дихотомических вопроса, всегда можно разделить на 4 группы (обозначим их a, b, c и d). В группу a входят ответившие «Да» на оба вопроса, в группу b – ответившие «нет» на 1-й вопрос и «да» на 2-й вопрос, в группу c – ответившие «да» на 1-й вопрос и «нет» на 2-й, в группу d – ответившие «нет» на оба вопроса. Обозначим буквами a, b, c и d число человек в каждой группе и перепишем результаты опроса в следующую таблицу сопряженности:
| Ответ на 1-й вопрос | |||
| Да | Нет | ||
| Ответ на 2-й вопрос | Да | a | b |
| Нет | c | d |
Простейшим коэффициентом связи номинальных признаков является коэффициент ассоциации Юла. Он вычисляется по следующей формуле: 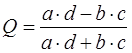 .
.
Вычислим в качестве примера коэффициент Юла для опроса, данные которого представлены в следующей таблице:
| Пью | Не пью | |
| Курю | ||
| Не курю |
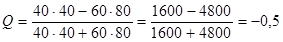
Коэффициент Юла может принимать значения от -1 до 1. Коэффициент Юла не может быть по модулю больше 1, потому что сумма, стоящая в знаменателе всегда по модулю больше разности, стоящей в числителе. Коэффициент Юла близок к 1 тогда, когда в таблице произведение a и d значительно больше произведения b и c. А это наблюдается тогда, когда респонденты при ответе «Да» на первый вопрос выбирают ответ «да» и на второй вопрос, а если отвечают на первый вопрос «нет», то на второй вопрос они тоже отвечают «нет». То есть, когда наблюдается 100%-ная положительная связь (если да, то да, а если нет, то нет). Коэффициент Юла близок к -1 тогда, когда, наоборот, произведение b и с значительно больше, чем произведение a и d. Эта ситуация возникает тогда, когда при ответе «Да» на первый вопрос респонденты, как правило, на второй вопрос отвечают «нет», а при ответе «нет» на первый вопрос респонденты выбирают на ответ второй вопрос «да». То есть, связь есть, но она отрицательная. Связь отсутствует тогда, когда коэффициент Q равен 0, например, в ситуации, когда a=b=c=d, или когда a=b и c=d, или когда a=c и b=d. Обычно наличие связи считается установленным, если коэффициент Юла по модулю больше 0, 5
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Другим коэффициентом, который можно вычислить для определения силы связи двух дихотомических признаков, является коэффициент контингенции. Он вычисляется по следующей формуле: 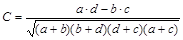 . Этот коэффициент может изменяться также в пределах от -1 до 1. При отсутствии связи значение коэффициента контингенции близко к 0. Величина коэффициента контингенции всегда меньше по модулю, чем величина коэффициента Юла. Обычно считается, что связь есть, если величина коэффициента контингенции по модулю больше 0, 3. В нашем примере
. Этот коэффициент может изменяться также в пределах от -1 до 1. При отсутствии связи значение коэффициента контингенции близко к 0. Величина коэффициента контингенции всегда меньше по модулю, чем величина коэффициента Юла. Обычно считается, что связь есть, если величина коэффициента контингенции по модулю больше 0, 3. В нашем примере
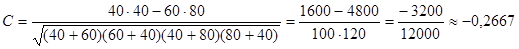
Коэффициент Юла равен 1 тогда, когда значение только одной ячейки равно нулю. Это было бы, например, если в нашем примере не встретилось пьющих, но не курящих (с=0). Это обозначало бы, что если человек пьет, то он обязательно курит. А если он не пьет, он может как курить, так и не курить. Тем не менее, значение Q указывает на 100%-ю связь. Поэтому говорят, что коэффициент Юла измеряет силу односторонней связи. Коэффициент контингенции в данном примере будет меньше 1. Он будет равен 1 только если равны нулю будут и b, и c. Поэтому считается, что коэффициент контингенции измеряет силу двусторонней связи.
Чтобы нагляднее продемонстрировать наличие или отсутствие связей, можно в ячейки таблице сопряженности записывать не количество ответов, а различные проценты. Это, например, могут быть проценты от общего числа людей, выбравших данный вариант ответа на один из вопросов. Перепишем таблицу сопряженности из примера, разобранного выше, в процентах по вопросу «курю - не курю»:
| Пью | Не пью | |
| Курю | 40/(40+60)=40% | 60/(40+60)=60% |
| Не курю | 80/(80+40)=66, 7% | 40/(80+40)=33, 3% |
Суммы по строке при такой записи везде должны получаться равными 100%. По процентам видно, что среди курящих в данной выборке оказалось 40% пьющих, а среди не курящих – 66, 7%. Если бы связи не было, процент пьющих среди курящих и не курящих оказался бы одинаков.
Аналогичные проценты можно вычислить и по столбцам, т.е. от числа людей, выбравших данный вариант ответа на 2-й вопрос. В 1-й ячейке тогда этот процент будет равен 40/(40+80)=33, 3%. Остальные проценты вычислите самостоятельно.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Те же методы, в том числе и вычисление процентов по строке и по столбцу, можно использовать и в таблицах сопряженности с размерностями большими, чем 2х2. Однако вычисление коэффициентов Юла и контингенции в этих случаях возможно только после сведения таблицы к виду 2х2, например, таким образом:
| Один из вариантов ответа на 1-й вопрос | Остальные варианты ответа на 1-й вопрос | |
| Один из вариантов ответа на 2-й вопрос | a | b |
| Остальные варианты ответов на 2-й вопрос | c | d |
Приведу еще несколько примеров того, как могут выглядеть таблицы сопряженности в случаях, когда связь существует и когда ее нет.
В левых трех таблицах связи между признаками нет, а в правых трех связь существует. Чтобы в этом убедиться, вычислите проценты по строке для всех таблиц.
|
|
