Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Вопрос 12.Оценка средних параметров. Меры разброса.

То, какие величины можно применять для оценки средних параметров, а какие нельзя, зависит от типа шкалы. В самом деле, среднее арифметическое значение пола вряд ли будет иметь смысл. Тем не менее, оценить средние параметры имеет смысл для любой шкалы. Оценку средних параметров еще называют измерением центральной тенденции. Эта задача, наряду с оценкой разброса значений, входит в раздел описательной статистики и является одним из первых шагов при обработке социологического опроса.

При номинальной шкале измерения мы можем лишь указать наиболее популярный ответ. Наиболее популярный ответ называется модой. Моду можно вычислить и при любой шкале. Однако это будет иметь смысл делать только тогда, когда число опрошенных значительно больше, чем число вариантов ответов. Действительно, если например, измерять рост в миллиметрах, то у всех 100-200 опрошенных окажутся разные значения роста. Модами тогда окажутся все эти варианты (они же будут максимально популярными!).

Имейте в виду, что мода – это вариант ответа, а не число человек, которые выбрали этот вариант. Также имейте в виду, что мод может быть несколько (как в предыдущем примере).

Если шкала порядковая, то помимо моды можно вычислить также медиану. Поясним смысл медианы. При порядковой шкале все варианты ответов можно расположить в порядке возрастания некоторого признака. Если это сделать, то какой-то ответ окажется в середине этого списка. Этот ответ и будет медианой. Другими словами, медиана – это ответ, стоящий в середине упорядоченной выборки. Медиана – это вариант ответа, а не то, сколько раз этот ответ встречается в выборке. Медиану можно вычислить и при интервальных шкалах, поскольку эти шкалы также позволяют расположить ответы в порядке возрастания. Для номинальной шкалы вычислить медиану нельзя! О способах вычисления медианы будет более подробно рассказано ниже на примерах.

Для интервальных (метрических) шкал оценкой средних параметров является среднее арифметическое значение. Оно равно сумме всех значений, деленной на число этих значений: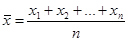

Среднее арифметическое более точно отражает средние параметры выборки, чем медиана, поскольку медиана не учитывает величины отклонений отдельных измерений от средних показателей. Ни для порядковой шкалы, ни для номинальной шкалы среднее арифметическое значение вычислить нельзя. Ведь сумма значений для этих шкал не имеет смысла, даже если ее можно формально вычислить, просуммировав коды ответов.

Для дихотомической шкалы в качестве меры средней тенденции возможно использовать только моду – какой из ответов более популярен.

Объединим рассказанное выше в таблицу:

Другими оценками средних значений для интервальных шкал для выборки из n значений могут служить:

среднее геометрическое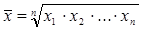

с реднее гармоническое ,

среднее квадратичное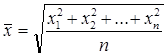

Взвешенное среднее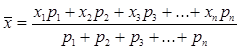

При вычислении взвешенного среднего предполагается, что каждому значению x_i придается некоторый весовой коэффициент p_i, больший или меньший единицы. Если бы все респонденты входили с равным весом, у всех x_i были бы коэффициенты p_i=1, а взвешенное среднее было бы равно среднему арифметическому значению. Часто взвешенным средним называют среднее арифметическое значение, вычисляемое по данным, сгруппированным в виде частотной таблицы – тогда веса p_i равны числу человек, выбравших i-й вариант ответа. Это будет показано и далее, на примерах вычисления среднего значения.

Все указанные выше четыре типа средних значений встречаются гораздо реже, чем среднее арифметическое. Как правило, при обработке обычных социологических опросов их не требуется вычислять. Такая необходимость может возникнуть, если распределение величины X отличается от нормального (см. далее), при неодинаковом отношении к отдельным респондентам или группам респондентов и т.д.

Помимо оценки средних показателей выборки необходимо оценить, насколько сильно могут отличаться данные отдельных респондентов от этих средних показателей. Например, мы получили среднее значение роста респондентов 170 см. Однако, это значение могло быть получено для группы, в которой все имеют одинаковый рост 169-171 см, а могло быть получено там, где есть и 150-сантиметровые карлики, и двухметровые гиганты. Во второй выборке разброс явно выше. Из данного примера видно, что среднее значение без мер разброса недостаточно хорошо описывает свойства выборки и популяции. И речь идет не только об измерениях по интервальной шкале. Одна группа может проголосовать «за» практически единогласно, а другая – на 51% (остальные – «против»), а мода в обоих случаях будет одна и та же («за»).

Простейшей оценкой разброса данных по номинальной шкале может служить разность количества ответов в наиболее и наименее популярных вариантах. Пусть, например, в опросе были получены данные: «зимой» – 10 ответов, «весной» – 50 ответов, «летом» – 20 ответов, «осенью» - 20 ответов. Наиболее популярным является ответ «весной», наименее популярным – «зимой». Разность количества ответов будет равна 50-10=40. Для того, чтобы этот коэффициент был более наглядным, часто его выражают как отношение 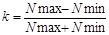, то есть разность числа людей, выбравших наиболее и наименее популярные ответы, деленная на сумму числа людей, выбравших эти варианты. В нашем примере 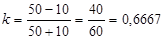. Нетрудно убедиться, что данный коэффициент равен 1, если все респонденты выбрали только один вариант. Если же все варианты были выбраны равным числом респондентов, то этот коэффициент равен нулю. В остальных случаях значения коэффициента лежат между 0 и 1. Недостатком k служит то, что на его величину никак не влияют ответы, выбранные не максимальным и не минимальным числом человек. Поэтому оказалось целесообразным ввести еще один коэффициент, который назвали коэффициент качественной вариации.

Пусть шкала дихотомическая и возможно только два варианта ответа, которым соответствуют числа респондентов N₁ и N₂ из общего числа N=N₁+N₂. Произведение 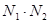, или 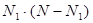при заданном N минимально (равно 0) тогда, когда все выбрали только один ответ. Максимальное значение 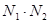достигается, если оба ответа выбраны одинаковым числом человек, т.е. когда N₁=N₂=N/2. Значение этого произведения равно 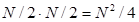. Вы можете сами в этом убедиться, построив значение 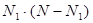графически в зависимости от N₁ при фиксированном N. Коэффициент качественной вариации для дихотомической шкалы равен отношению произведения 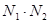к его максимальному значению: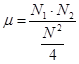

Теперь обобщим смысл коэффициента качественной вариации на общий случай номинальной шкалы (k вариантов ответа). Сверху в коэффициенте μ будет располагаться сумма всевозможных произведений вида Ni*Nj, то есть 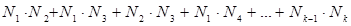. В знаменателе должно стоять максимальное значение такой суммы, т.е. значение для ситуации, когда все ответы были выбраны равным числом респондентов. Для k вариантов и выборки объема N это число равно N/k человек. Значение произведения в таком случае равно 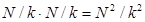. Число произведений вида 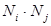вычисляется из комбинаторики (как число сочетаний из k элементов по 2) и равно 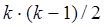. В итоге получается следующая формула для коэффициента качественной вариации:

Вычислим коэффициент качественной вариации для предыдущего пример а. У нас 4 варианта ответа (зима, весна, лето, осень), поэтому k=4. Было опрошено N=10+50+20+20=100 человек. Подставляем в формулу:

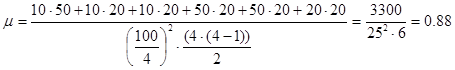
Коэффициент качественной вариации имеет смысл вычислять тогда, когда число вариантов ответа не слишком велико. Шкала при этом, как правило, номинальная. Диапазон изменения коэффициента – от 0 (выбирали только один из ответов) до 1 (всех ответов выбрано поровну).

Для порядковой шкалы мерой разброса может служить квартильный размах.

Для начала введем понятие квартилей. Медиана – это значение (вариант ответа), которое делит упорядоченную (!) выборку на две равные части. А при делении выборки не на две, а на 4 равные части можно найти три значения (для 25%, 50% и 75%), имеющие сходный смысл. Они и называются квартилями. Одним из квартилей (для 50%) является медиана. Два другие квартиля (25% и 75%) ищутся методами, аналогичными медиане. То есть, если данные представляют собой список значений, то его надо сначала переписать в порядке возрастания признака, а затем определить, какие значения находятся на 25% и 75% этого списка. Если данные сгруппированы в частотную таблицу, то квартили ищутся также аналогично медиане, но вместо 50% надо использовать уровни 25% и 75%. Разность квартилей 75% и 25% называется квартильным размахом.

Вычислим квартильный размах для примера, разобранного нами при изучении медианы. Список данных 7, 10, 12, 5, 6, 6, 3, 15, 12, 11, 14, 8, 9 (всего 13 значений) сначала переписываем в порядке возрастания: 3, 5, 6, 6, 7, 8, 9, 10, 11, 12, 12, 14, 15.

На уровне 25% (3 числа от начала) лежит число 6, на уровне 75% - число 12.

Значит, квартили для 25% и 75% равны соответственно 6 и 12. Квартильный размах равен 12 – 6 = 6.

Мерами разброса для интервальной шкалы служат дисперсия и стандартное отклонение. Смысл данных мер разброса поясним на числовой прямой.

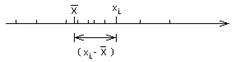
Разброс характеризуется отклонениями экспериментальных значений x_i от среднего значения. Например, если среднее значение равно 15, а x_i=17, то отклонение =17-15=2.

Сумма всех отклонений всегда равна 0, поэтому средняя величина отклонения не может быть взята за меру разброса. Используют средний квадрат отклонения, который называют дисперсией. Дисперсия вычисляется по формуле:

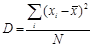, или

Неудобством использования дисперсии является то, что если, например, рост измеряется в сантиметрах, среднее значение роста – в сантиметрах, то дисперсия по росту будет иметь размерность квадратных сантиметров. Поэтому для оценки разброса значений чаще используют не дисперсию, а квадратный корень из дисперсии, называемый стандартным отклонением, или среднеквадратичным отклонением.

В некоторых учебных пособиях стандартное отклонение обозначается буквой σ, а дисперсия σ ². В некоторых учебниках буквой σ обозначается дисперсия. Во избежание путаницы я призываю запоминать формулы по смыслу. Подытожим в таблице, какими мерами разброса можно пользоваться для каких шкал: